Il teorema di Bernoulli in fluidodinamica
Una delle leggi più importanti della fluidodinamica è il teorema di Bernoulli (anche equazione di Bernoulli o principio di Bernoulli), che prende il nome dall’omonimo fisico svizzero vissuto durante il XVIII secolo.
Daniel Bernoulli era già figlio di un matematico rinomato per l’epoca, ma si dimostrò di gran lunga più intuitivo e abile del padre. Pare addirittura che quest’ultimo tentò di far passare come proprio uno dei libri scritti dal giovane.
Oltre alle sue ricerche sulla fluidodinamica questo fisico è ricordato anche per il contributo che diede allo studio della Statistica. Tentò anche di utilizzare questo approccio per dimostrare l’efficacia del vaccino contro il vaiolo elaborando i dati sulla mortalità della malattia.
Ma cosa enuncia il teorema di Bernoulli?
Cosa dice il teorema di Bernoulli
Per cominciare vediamo di introdurre a dovere questa legge, forse la più importante nell’ambito della dinamica dei fluidi.
La legge di Bernoulli si applica a tutti i fluidi ideali, ovvero incomprimibili (a differenza dei gas) e non viscosi. La fluidità è l’attrito interno fra le particelle del fluido, ma è una caratteristica propria solo dei fluidi reali. Quelli ideali ne sono del tutto privi.
Immaginiamo ora di avere un condotto dove scorre un fluido che non rimane costante per altezza e sezione, ma variabile. Considerando due punti del condotto che abbiano sezione e altezza variabile indiciamo le prima con S1 e S2 e le seconde con h1 e h2.
Per formulare il teorema di Bernoulli ci occorre anche definire le due pressioni P1 e P2 con cui scorre il fluido, e le velocità v1 e v2.
Indicando infine con la lettera greca ρ la densità del fluido, possiamo procedere a esaminare la formula espressa sotto forma di equazione.
Avremo P1 + 1/2ρv12 + ρgh1 = P2 + 1/2 ρv22+ ρgh2.
Poiché nonostante consideriamo due punti diversi il risultato rimane uguale si può anche dichiarare che per ogni punto del condotto la somma dei termini P + 1/2ρv + ρgh rimane costante.
La g presente nel terzo termine è l’accelerazione di gravità, pari a 9,81 m/s².
Le due altezze h1 e h2 si misurano in metri, la pressione si esprime in Pascal (Pa) mentre la densità ρ può variare fra g/cm³ o kg/m³.
Quali sono le possibili applicazioni fisiche del principio di Bernoulli
Oltre a consentire di studiare delle situazioni quotidiane e gli eventi naturali, ma lo si può applicare per costruire apparecchiature tecnologiche.
Quando si preme il palloncino posizionato in cima l’aria scorre all’interno di un tubicino sottile rispetto al volume della boccetta.
La differenza di pressione spinge il liquido verso l’alto e incontrando il getto d’aria forma delle goccioline di profumo nebulizzato. Lo stesso principio vale per le bombolette spray di deodorante che si usano oggi.
Ma oltre che negli oggetti una conferma del teorema di Bernoulli si può trovare anche nel sistema circolatorio. Quando si formano degli accumuli di colesterolo nelle arterie la sezione del vaso sanguigno si riduce e la pressione interna si abbassa. Questo spiega perché la circolazione diventa più difficile. In questo caso si può trascurare però il valore di g.
Applicando il teorema alle correnti d’aria si può usarlo anche per spiegare il volo degli aeroplani.
La forma delle ali è studiata per far sì che l’aria che passa sulla parte superiore sia più veloce di quella che incontra la parte inferiore.
Questo favorisce il decollo del mezzo.
Esercizio sul teorema di Bernoulli
Vediamo un caso pratico di applicazione dell’equazione vista al primo paragrafo. Supponiamo di avere un tubo disposto in orizzontale la cui sezione si restringa ad un certo punto. La prima, S1, è più larga e presenta raggio pari a 1 m, mentre la seconda, S2, di 60 cm. Velocità e pressione cambiano in corrispondenza dei due tratti di tubo di larghezza diversa.
Forniamo i dati relativi alla velocità nel punto più largo (5 m/s), e le due pressioni P1 e P2, rispettivamente di 1,2 x 105 e 0,3 x 105. L densità dell’acqua pura, che terremo come riferimento, è 1000 kg/m³. Dato che il tubo è disposto in orizzontale non ci sono variazioni in termini di altitudine e perciò h1 = h2. Il parametro può essere rimosso dall’equazione del teorema di Bernoulli.
Useremo perciò la formula P1 + 1/2ρv12 + ρg = P2 + 1/2 ρv22+ ρg. Semplifico ulteriormente togliendo ρg dall’equazione. Rimane perciò P1 + 1/2ρv12 = P2 + 1/2 ρv22 ed esplicitando v22 dovrei fare 2/ρ(P1-P2) + v12. Sostituendo i dati 2/1000[(1,2 -0,3) x 105] + 52. Viene fuori 205, ma per trovare il valore di v2 serve fare la radice quadrata. Quindi √205 = 14,31 m/s.
Che cos’è l’effetto Venturi: il paradosso idrodinamico
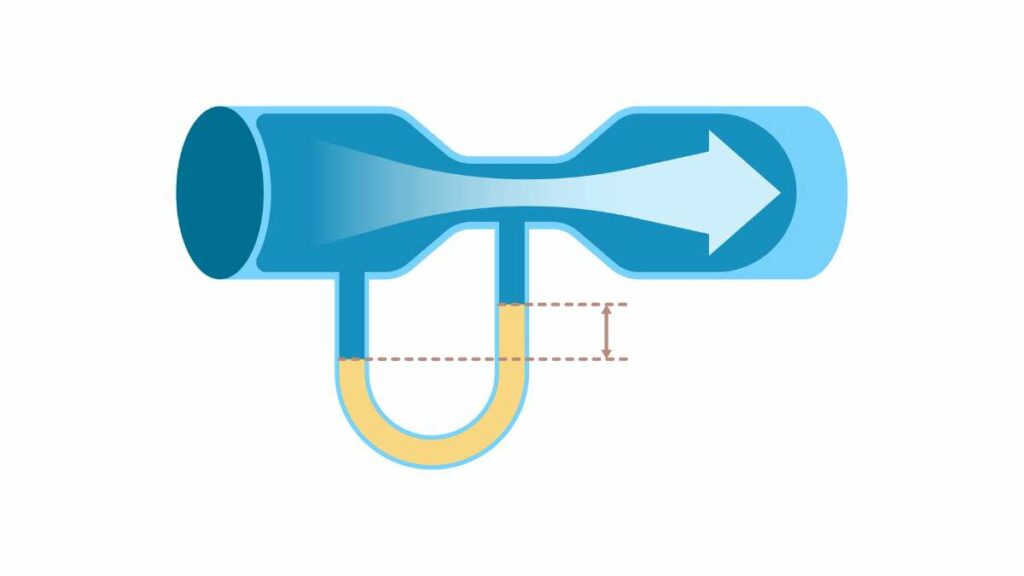
Più comunemente lo si chiama effetto Venturi e riguarda tutti i fluidi che scorrono lungo una conduttura orizzontale che presenta dei punti in cui la sezione si allarga e altri in cui si restringe.
Come prima, il parametro h si rimuove dall’equazione.
Si tratta di un condotto orizzontale dove è presente una strozzatura centrale. Sia a livello della sezione più larga che sulla strozzatura sono collegati due manometri.