Le correnti che attraversano un circuito elettrico: le leggi di Kirchhoff
Per studiare le correnti che attraversano un circuito elettrico ci servono le leggi di Kirchhoff, due equazioni che spiegano la conservazione della carica. La prima è nota anche con la definizione di legge dei nodi, mentre la seconda sui libri di Fisica compare come legge delle maglie. Avere presenti i concetti di nodo e di maglia quindi è essenziale per poterle comprendere.
Il fisico tedesco a cui sono attribuite le formulò entrambe nel 1845 quando ancora non era laureato, dato che conseguì il titolo nel 1847. Una volta ottenuta la cattedra all’Università di Heidelberg sviluppò lo spettroscopio insieme al chimico Robert Bunsen. Scoprì inoltre due nuovi elementi della tavola periodica, ovvero il cesio (Cs) e il rubidio (Rb).
Le leggi di Kirchhoff e i circuiti ohmici
I due principi noti con questo nome valgono per i circuiti elettrici che soddisfano le condizioni per essere considerati ohmici. Le caratteristiche da rispettare sono due, di cui la prima è quella per cui il circuito risulti collegato a un generatore di tensione che rilascia una corrente continua (CC). Per corrente continua si intende un flusso di carica che si mantiene costante nel tempo e che non cambia la propria direzione.
La seconda condizione richiesta ai circuiti ohmici è quella di essere costituiti da resistori per cui vale la prima legge di Ohm. Senza sovrapporla alle leggi di Kirchhoff si tratta del principio per cui la differenza di potenziale in un circuito è data dal prodotto della resistenza per l’intensità di corrente.
In formula la scriviamo nella forma ΔV = Ri.
I resistori interni al circuito possono essere collegati sia in serie che in parallelo. Nel primo caso la resistenza equivalente è data dalla somma delle singole resistenze, mentre nel secondo caso è il risultato della somma dei loro reciproci. Ricordiamo che nei circuiti di questo tipo vale l’effetto Joule, quindi si verifica sempre una dissipazione di energia almeno sotto forma di calore.
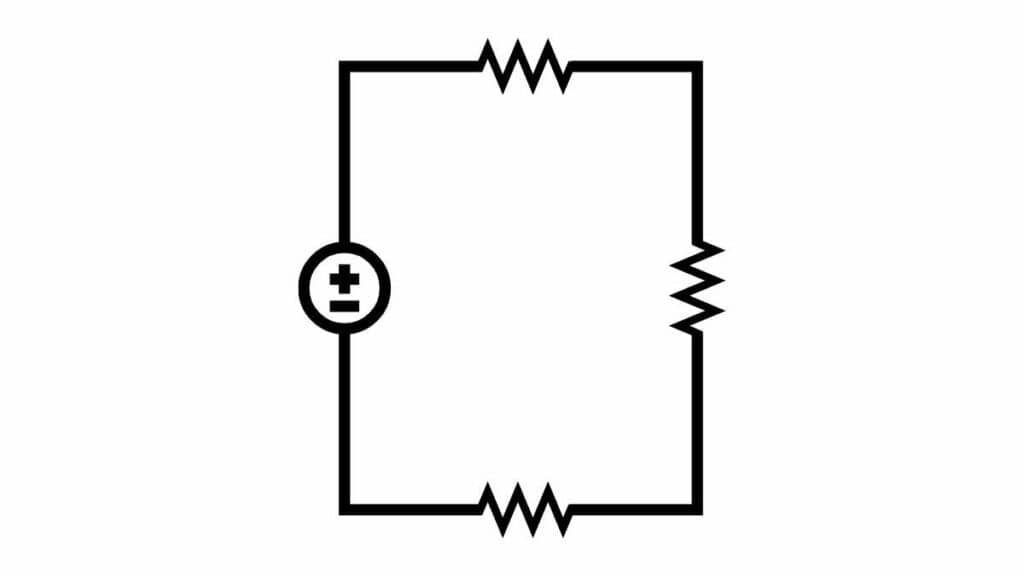
A questo punto possiamo definire anche cosa siano i nodi e le maglie. Il nodo in un circuito elettrico è il punto in cui un cavo si dirama in più di un filo o viceversa il punto in cui più fili si raggruppano in un solo cavo. La maglia invece è uno dei possibili percorsi chiusi che la corrente percorre all’interno del circuito.
La legge dei nodi
La prima delle leggi di Kirchhoff indaga l’intensità delle correnti che entrano in un nodo del circuito ohmico. Non ci sono vincoli al numero di fili in cui può diramarsi un cavo né su quelli che possono convergere nello stesso conduttore.
L’enunciato della legge afferma che la somma delle correnti che entra in un nodo è uguale a quella delle correnti uscenti.
Usando il simbolo della sommatoria Σ quindi in formula possiamo scrivere nΣie = mΣiu, dove Σie è il totale delle correnti entrati e Σiu la somma delle correnti uscenti. I coefficienti n e m corrispondo rispettivamente al numero di correnti entranti e a quello dei flussi uscenti dal medesimo nodo. O, per essere più pratici, al numero di fili.
Per vedere una prima applicazione pratica delle leggi di Kirchhoff supponiamo di avere un nodo dove ci sono due cavi che entrano e quattro che escono. Numerando le correnti da 1 a 6, di cui le prime due sono entranti e le restanti quattro risultano uscenti otterremo l’uguaglianza che segue. Ovvero i1 + i2 = i3 + i4 + i5 + i6. Nei nodi quindi non avvengono dispersioni di corrente, almeno a livello complessivo.
Una formulazione alternativa di questo principio dei circuiti ohmici è “la somma algebrica delle correnti che convergono nello stesso nodo è nulla“. Questo enunciato vale considerando positivi i flussi di carica entranti e negativi quelli che si allontanano dal nodo.
La legge delle maglie
In formula possiamo scrivere questo principio nella forma ΣΔVk = 0. Si potrebbe pensare che ci sia una sola differenza di potenziale creata dal generatore, ma in realtà ci sono anche quelle presenti ai capi delle varie resistenze. Si chiamano anche cadute di tensione ed esistono dei calcolatori appositi per stimarla, essenziali quando si progetta un impianto elettrico.
Per individuare le maglie si parte dal polo positivo del generatore di corrente e si procede verso quello negativo. A ogni maglia per applicare la seconda delle leggi di Kirchhoff bisogna anche assegnare un senso da seguire, che può essere orario o antiorario. Quando si incontra una resistenza se la corrente la percorre secondo il verso indicato prima allora la ΔV è positiva. Se opposto, è negativa.