Il volume di una piramide a base quadrata in geometria solida
Gli studenti fanno sempre un salto sulla sedia vedendo “volume piramide a base quadrata” scritto sulla lavagna a inizio lezione. In effetti rispetto al calcolo delle dimensioni di un parallelepipedo o un cubo la sua formula è più complessa, ma basta fare pratica con gli esercizi per memorizzarla.
Il solido di cui parliamo ha un certo rilievo storico considerando che la maggior parte delle piramidi egizie ha questa forma, tra cui la celebre Piramide di Cheope. Si tratta di una delle Sette Meraviglie del Mondo Antico, visitata ogni anno da milioni di persone. La sua regolarità esprime la perfezione del divino.
Volume piramide a base quadrata: struttura del solido
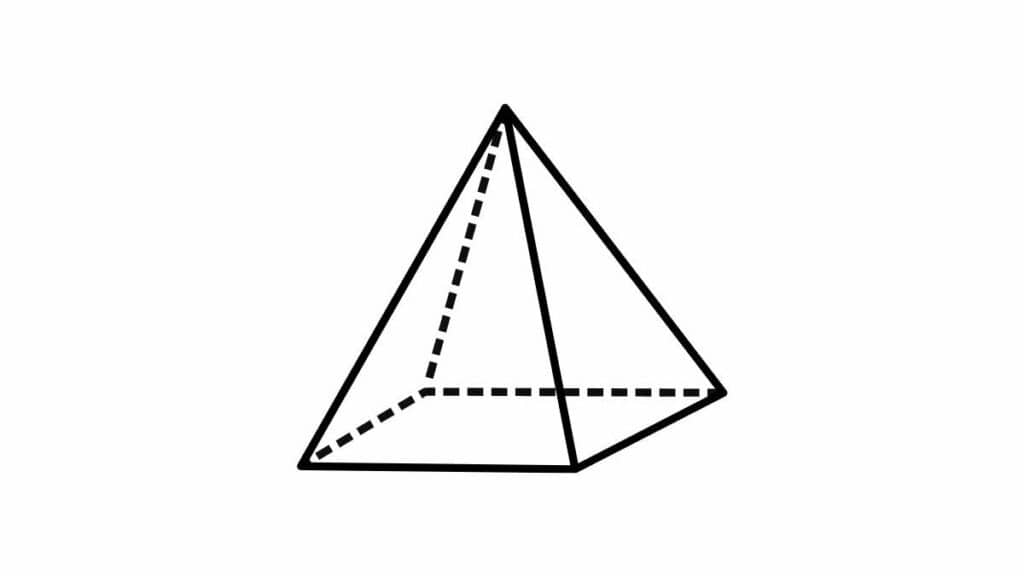
Si definisce piramide un poliedro che ha una base costituita da un poligono qualsiasi e da facce laterali di forma triangolare. Questi triangoli uniscono la base con un vertice rappresentato da un punto esterno al piano della base. Nel caso di quella che ha un quadrato come base si tratta di una piramide regolare, anche se può essere sia retta che obliqua.
Quando è retta significa che all’interno del poligono di base si può inscrivere un cerchio e che il piede dell’altezza del solido coincide con il suo centro.
La formula del volume piramide a base quadrata non cambia a seconda che essa sia retta o obliqua, un piccolo dettaglio che va precisato. Quando è obliqua i triangoli della superficie laterale hanno altezze diverse fra di loro.
In una piramide retta che ha per base un quadrato tutti i triangoli che uniscono la base al vertice esterno sono isosceli e congruenti fra di loro. L’altezza di questi triangoli isosceli si dice apotema della piramide. La sua misura si calcola per ogni piramide dividendo il doppio dell’area della superficie laterale per il perimetro di base.
Nel caso della piramide obliqua invece il piede dell’altezza non coincide con il centro del quadrato di base ma è un punto esterno a questo poligono. La si disegna tracciando la retta perpendicolare che unisce il vertice della piramide con il piano su cui giace la base della figura tridimensionale.
Quali sono le misure richieste dalla formula
Per trovare il volume della piramide a base quadrata bisogna prima vedere quali sono le grandezze che dobbiamo conoscere per calcolarlo. Eccole di seguito:
- Superficie dell’area di base (Ab o Sb). Dato che in questo caso particolare la base è un quadrato la sua area si può ricavare semplicemente conoscendo la misura dello spigolo ed elevandola al quadrato. Quindi chiamando l lo spigolo di base possiamo scrivere Ab =l2.
- L’altezza della piramide (h). Abbiamo descritto al paragrafo precedente di che cosa si tratta, sia nel caso della piramide retta che nel caso in cui il solido è obliquo. Per ricavarla si può utilizzare la formula inversa del perimetro, ma non solo. Conoscendo l’apotema della figura (a) e il raggio del cerchio (r) inscritto nella base si può fare h = √a2 – r2 secondo il teorema di Pitagora.
Per trovare il raggio del cerchio inscritto nella base, in una piramide retta a base quadrata basta un calcolo semplice. Infatti il centro del cerchio e quello del quadrato fra di loro sono congruenti e corrispondono a metà dello spigolo di base. Di conseguenza è lungo la metà del lato e per ricavarlo basta fare r = l/2.
Invece l’apotema in questa figura 3D come per l’altezza ricava ragionando sul fatto che si tratta dell’ipotenusa del triangolo rettangolo che forma con l’altezza e il raggio. Per trovarla quindi si fa a = √h2 + r2.
Volume della piramide a base quadrata: la formula
La formula, indicando con V il volume, si scrive V = (Ab x h)/3.
Moltiplicando l’area di base per l’altezza infatti si trova il volume di un parallelepipedo composto da 3 piramidi come quella che si sta esaminando. In alternativa conoscendo lo spigolo e l’altezza si può scrivere anche V = (l2 x h)/3.
Vediamo ora la formula inversa per ricavare l’altezza del volume.
Partendo da V = (Ab x h)/3 dobbiamo moltiplicare il volume per il numero 3 e dividerlo per la superficie dell’area di base. Quindi scriveremo h = 3V/Ab. Oppure usando la seconda formula h = 3V/l2.
Supponiamo ora di trovare un esercizio dove sono noti il volume piramide a base quadrata e la sua altezza ma non l’area di base.
Partendo sempre dalla prima formula dovremo sempre moltiplicare V per tre e successivamente dividere il risultato per a misura dell’altezza. Dunque faremo Ab = 3V/h.
Per trovare direttamente la misura dello spigolo dato che l’area di base è il suo quadrato è sufficiente fare la radice quadrata della formula inversa per Ab. Bisogna perciò fare il calcolo l = √3V/h.