Il Teorema di Lagrange in analisi matematica
In Analisi Matematica l’ambito dello studio di funzione è ampio e in esso rientra anche l’applicazione del Teorema di Lagrange. Spesso lo si considera semplicemente un’estensione o meglio generalizzazione del Teorema di Rolle. Questo perché esso definisce il comportamento delle funzioni derivabili e continue all’interno di un intervallo chiuso e limitato, esattamente come la regola che esamineremo di seguito.
A formularlo fu un matematico e astronomo di origine italiana naturalizzato in Francia, noto come Joseph-Louis Lagrange. Nel campo della Matematica studiò in particolare le equazioni differenziali e l’analisi infinitesimale, mentre in Fisica si concentrò sulla meccanica razionale. Il teorema sulle funzioni che porta il suo nome risale al 1691.
Enunciato e formula del Teorema di Lagrange
Partiamo dalla sua forma estesa per poi scendere nel dettaglio e rappresentarlo tramite formula. Questa estensione del teorema di Rolle considera una funzione f(x) continua e derivabile in un intervallo [a,b] dove a < b. All’interno di tale intervallo afferma che esiste un punto c in cui derivata f'(x) coincide con il coefficiente angolare della retta che congiunge gli estremi, ovvero a e b.
Volendo rappresentarlo in formula possiamo scrivere che f'(c) = f(b) – f(a)/b – a. Per dimostrarlo possiamo considerare una funzione ausiliaria, detta φ(x) definita come f(x) -f(a) – f(b) – f(a)/b – a (x – a). Va premesso che f(x) è continua e derivabile nell’intervallo [a,b] ed f(a), f(b) – f(a)/b – a e (x – a) sono continui e derivabili nell’insieme R. Inoltre vale φ(a) =φ(a) e φ risulta continua in [a,b] e derivabile in ]a,b[.
Ora dimostriamo il teorema di Lagrange calcolando la derivata φ'(x) = f'(x) – f(b) – f(a)/b – a. A questo punto possiamo calcolare la derivata di φ(x) nel punto c e porla uguale a zero, quindi φ'(c) = f'(c) – f(b) – f(a)/b – a = 0. Possiamo perciò determinare che f'(c) = f(b) – f(a)/b – a portando l’espressione a destra dell’uguale.
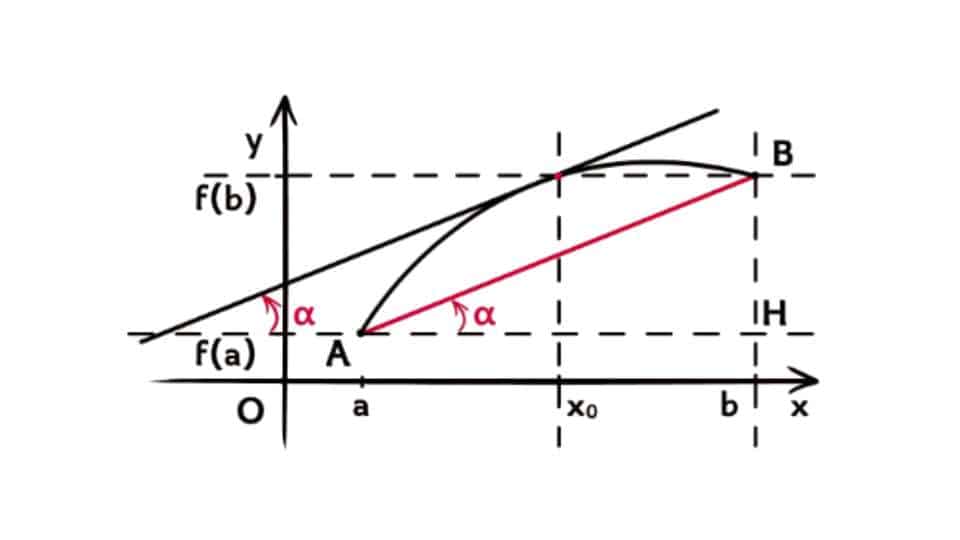
Analizzando questa regola dal punto di vista geometrico possiamo riformulare l’enunciato come segue. Ovvero nell’intervallo che stiamo esaminando esiste almeno un punto P (c, f(c)) per cui passa una retta tangente alla corda che possiamo tracciare dal punto A fino al punto B.
Due esempi pratici
Proviamo ora ad applicare il teorema di Lagrange prendendo una funzione f(x) = √6 – x, definendo un intervallo [4,6] e di voler trovare il punto c che soddisfi la condizione stabilita dal teorema. Dato che il dominio della funzione è nell’intervallo (-∞,6] si può lavorare nell’intervallo descritto. La funzione risulta continua e derivabile, quindi possiamo cercare c.
Vediamo che f(a) e f(b) sono rispettivamente f(4) e f(6), quindi le calcoliamo e troviamo che f(4) = √2 e f(6) = 0, mentre b – a = 2. Visto che f’c = f(b) – f(a)/b – a possiamo sostituire i dati nella formula e ottenere f'(c) = 0 – √2/3 = -√2/3. La derivata prima della funzione √6 – x invece è – 1/2√6 – x = -√2/3.
Sostituendo a x la c avremo 1/2√6 – c = -√2/3, e possiamo moltiplicare entrambi i membri per 6√6 – c in modo da trovare che 2√2 √6 – c = 3. Elevando al quadrato sia a sinistra che a destra dell’uguale si avrà 8(6 – c ) = 9 e quindi 6 – c = 9/8, da cui c = 39/8. Considerando invece la funzione f(x) = 1/x – 3 e l’intervallo [2,4]. Il dominio della funzione esclude il punto x = 3, in quanto annullerebbe il denominatore.
Di conseguenza la funzione considerata non è continua all’interno dell’intervallo e non è possibile applicare il teorema. Se avessimo considerato per esempio l’intervallo [4,6] avremmo invece potuto usarlo.
Differenze fra il teorema di Lagrange e di Rolle
Abbiamo detto all’inizio che possiamo considerare il teorema che stiamo studiando come un’estensione di quello enunciato da Rolle. Quest’ultimo considera sempre una funzione f(x) continua a derivabile in un intervallo [a,b]. L’enunciato afferma che se f(b) = f(a) allora nell’intervallo esiste un punto c interno all’intervallo dove f'(x) = 0.
Perché valga è necessario come per il teorema di Lagrange che la funzione risulti continua nell’intervallo stabilito oltre che derivabile in ogni punto compreso fra a e b. Il punto c indicato nell’enunciato considerando le condizioni può corrispondere a un massimo o un minimo locale, o essere un punto di flesso orizzontale. Vale a dire un punto in cui cambia la concavità del grafico della funzione.
Proviamo a vedere un esempio con la funzione f(x) = x2– 5 e l’intervallo [-1,1]. Il dominio della funzione è continuo in tutto R, e la derivata prima è f'(x) = 2x. Calcoliamo f(-1) = 1 – 5 = – 4 e f(1) = 1 – 5 = -4. Visto che è soddisfatta la condizione per cui f(b) = f(a) possiamo applicare Rolle. Quindi f'(c) 0 solo quando 2x = 0, quindi c è pari a 0.
Grazie al teorema di Rolle è facile localizzare i punti di massimo e di minimo di una funzione matematica. Trova però applicazioni possibili anche in Meccanica, in particolare per quanto riguarda lo studio del moto di un oggetto e i punti in cui la sua velocità si annulla. Nello studio dei cicli termodinamici ci dice invece i punti in cui la variazione di temperatura o pressione è uguale a zero.