Le tipologie di oscillatore armonico
In Fisica parlare di oscillatore armonico equivale a riferirsi a un qualsiasi sistema fisico che segua le leggi del moto armonico. Proprio perché si tratta di una definizione così generica esistono però più tipologie, di cui possiamo ricordarne tre: l’oscillatore semplice, quello smorzato e quello quantistico. Il primo è quello più studiato e corrisponde a una singola particella.
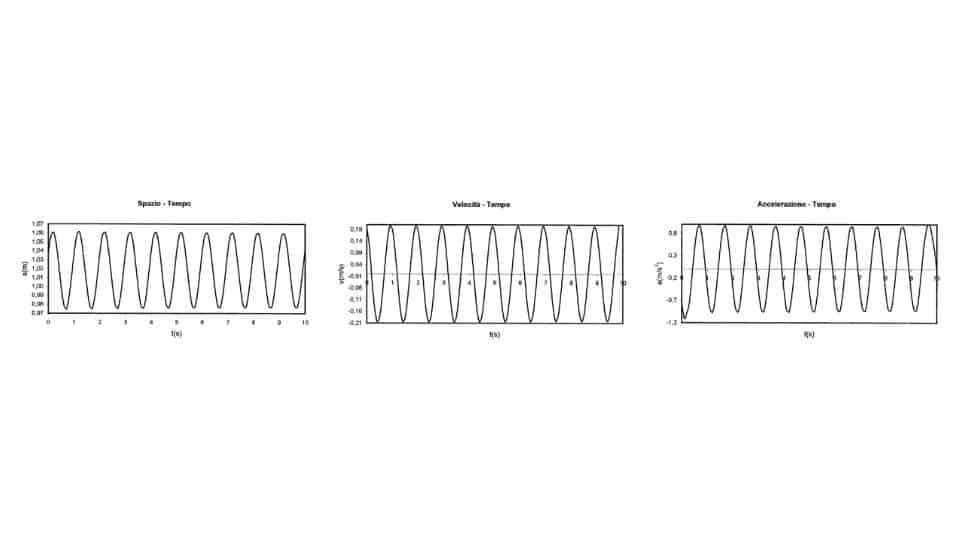
Dal punto di vista cinematico il moto armonico consiste nella proiezione del moto di un punto materiale che si muove lungo una traiettoria circolare sul diametro della stessa traiettoria. A questo punto però è ora di approfondire nel pratico questa tipologia di moto analizzando gli oggetti che seguono le sue leggi e vedere i diversi casi che si possono presentare.
Definire un oscillatore armonico
La legge oraria del moto armonico, ovvero la formula che ci dice come varia la posizione di un corpo in funzione del tempo, è x(t) = Acos(ωt + ϕ). In particolare A rappresenta l’ampiezza dell’oscillazione, cioè la distanza massima della proiezione dal centro della traiettoria. La velocità angolare ω qui si chiama pulsazione e infine ϕ rappresenta la costante di fase.
Un qualsiasi corpo che si muova seguendo questa legge oraria costituisce di fatto un oscillatore armonico. Un esempio classico che si fa per dare un’immagine concreta a questo concetto è quello di un peso agganciato a una molla in tensione, che oscilla lungo un piano privo di attrito. Una volta che si allunga la molla si genera forza elastica e il peso cerca di raggiungere una posizione di equilibrio.
Al tempo stesso anche la molla però si troverà spinta dall’oggetto appeso fuori dalla sua posizione di riposo. Di conseguenza in assenza di attrito e senza che siano presenti altre forze esterne le oscillazioni del corpo potrebbero proseguire all’infinito. La forza che provoca le oscillazioni è espressa dalla legge di Hooke, ossia F = -kx dove k è la costante elastica della molla. La sua direzione è opposta a quella dell’elongazione.
Nel caso della molla lo spostamento è rettilineo, ma nel caso del pendolo è angolare. In questo caso lo spostamento nella legge oraria non si esprimerà con x ma con θ, anche se usando la stessa formula.
L’equazione di una particella con moto armonico
Iniziamo ad esaminare il caso dell‘oscillatore armonico semplice, che corrisponde a una particella che esegue un’oscillazione armonica intorno a una posizione di equilibrio. Volendo si può anche ricorrere all’esempio del pendolo semplice, dove abbiamo un punto materiale sospeso tramite una fune a un punto fisso da cui questa oscilla.
A muoverlo è la forma elastica F = -kx, ma dato che la forza è data da massa per accelerazione possiamo scrivere -kx = ma. L’accelerazione a si può indicare anche come la derivata dello spostamento rispetto al tempo (d2x/dt2). Quindi la formula di prima si può riscrivere nella forma -kx = md2x/dt2. L’uguaglianza ottenuta si può riscrivere come equazione portando tutto a sinistra dell’uguale.
Si ottiene perciò -kx/m – md2x/dt2 = 0, che cambiando i segni diventa kx/m + md2x/dt2 = 0. Questa costituisce l’equazione differenziale dell’oscillatore armonico semplice, ma bisogna considerare che vale se sussiste la relazione ω2 = k/m. Di conseguenza per ricavare la pulsazione si usa la formula ω = √k/m. A questo possiamo riscrivere l’equazione differenziale in forma più semplice inserendo la pulsazione.
Otterremo perciò ω2x + md2x/dt2 = 0. Il periodo di oscillazione T invece nel limite di oscillazioni piccole si ottiene con la formula T = 2π/ω.
L’oscillatore armonico smorzato
Il caso esaminato al paragrafo precedente non è realistico perché considera un’oscillazione che si verifica in assenza di forze dissipative. Quando consideriamo la tipologia smorzata invece consideriamo la presenza di forze d’attrito, che per l’appunto ostacola le oscillazioni. In questo caso quindi non è possibile che il corpo considerato prosegua nel suo moto armonico all’infinito.
Quando abbiamo di fronte un oscillatore armonico smorzato l’ampiezza A tende a decrescere man mano che passa il tempo. Se abbiamo un punto materiale appeso a una molla che oscilla sul piano orizzontale la forza dissipativa è dovuta all’attrito con la superficie. Considerando invece un pendolo che oscilla invece a dissipare l’ampiezza delle oscillazioni troviamo l’attrito che questo ha con l’aria.
Nella sua equazione considerando il caso della molla avremo quindi sempre -kx e ma, ma a sinistra dell’uguale si aggiungerà la forza d’attrito. Possiamo scrivere μv, dove μ è il coefficiente e v la velocità, direttamente proporzionale alla forza di attrito. Ma possiamo scrivere la velocità come derivata dello spostamento rispetto al tempo ottenendo dx/dt.
L’equazione differenziale che risulterà quindi sarà d2x/dt2 + μ/m · dx/dt + ω2x. In caso il coefficiente di attrito risulti pari a zero allora μ/m · dx/dt risulterà nulla e si ritornerà all’equazione differenziale vista per l’oscillatore semplice. Nella legge oraria invece ad A sarà aggiunto un fattore esponenziale che indicherà la sua diminuzione nel tempo.
Come applicare il concetto a livello quantistico
Quando ci si addentra nella Fisica delle particelle scendiamo in un ambito puramente teorico. Una particella subatomica che si muove seguendo le leggi del moto armonico rappresenta un oscillatore armonico quantistico. In questo caso però a descrivere il comportamento del punto in movimento è l’equazione di Schrödinger. La si usa infatti per descrivere la posizione e il moto degli elettroni di un atomo intorno al suo nucleo.
Questa tipologia particolare di oscillatore ha una proprietà interessante rispetto ai due esaminati in precedenza. Trattandosi di una particella subatomica (elettrone) la sua energia è quantizzata, può perciò assumere solo valori discreti ben definiti. Inoltre la frequenza di oscillazione dipende dalla costante elastica, che fra di loro sono direttamente proporzionali.
Entrambe queste proprietà tornano utili nella progettazione dei circuiti oscillanti, definiti così perché il generatore eroga una forza elettromotrice che oscilla in maniera sinusoidale.