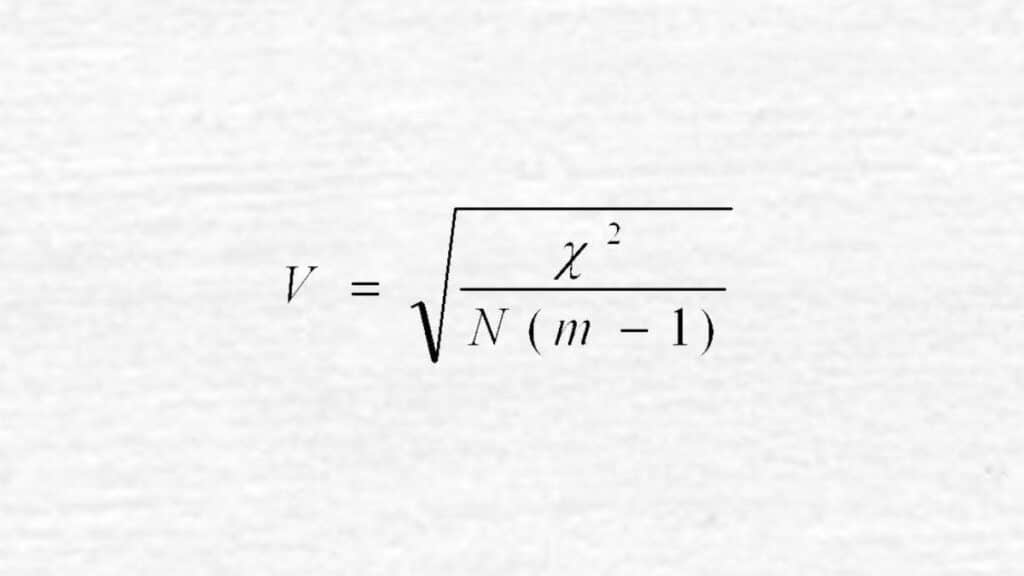Indice V di Cramer e l'associazione fra due variabili qualitative
Per studiare il grado di associazione fra due variabili qualitative si utilizza spesso l’indice V di Cramer. Il suo calcolo si basa sul test del Chi-quadrato e prende il nome dal matematico svizzero Carl Harald Cramér che lo inventò nel 1946. I valori che può assumere rientrano nell’intervallo fra 0 e 1, dove lo zero corrisponde a un grado nullo di associazione.
Quando invece il valore di V è uguale a uno significa che le due variabili o i due caratteri che si stanno considerando tra di loro sono in correlazione perfetta. Per indicare le due variabili si utilizzano X e Y.
Cos’è l’indice V di Cramer
Come abbiamo detto si tratta di una misura statistica che si può ricavare dal test del chi-quadrato (χ²). Si tratta di un sistema di verifica di ipotesi per valutare se le frequenze osservate in uno o più gruppo corrispondano alle frequenze attese. L’esempio classico per spiegare questo test è la frequenza dei caratteri per verificare la terza legge di Mendel (quella dell’assortimento indipendente).
Uno dei pregi di questa misura di associazione è che risulta chiara e facile da interpretare rispetto ad altri indicatori come il coefficiente di correlazione di Pearson. L’indice V di Cramer varia fra 0 e 1, mentre quello di Pearson fra i valori -1 e + 1, dove lo zero è la misura intermedia che corrisponde a una correlazione positiva e non a un’assenza di dipendenza fra i caratteri.
Per riuscire a trovare il valore dell’indice è necessario considerare le dimensioni della tabella di contingenza, ovvero il numero di righe e di colonne che presenta. La formula per calcolarlo è V =√ (χ2/n)/min[(n -1),(c – 1)] dove r e c indicano proprio le righe e le colonne di questa tabella. Il simbolo χ2 rappresenta valore del chi-quadro mentre n è la numerosità del campione.
Volendo si può dire in breve che il valore di V rappresenta la radice quadrata del Chi-quadrato normalizzato. Per interpretare il suo valore occorre fare riferimento sempre alla tabella di contingenza e in particolare ai gradi di libertà, ossia al denominatore della formula.
Un esempio pratico di applicazione di V
Proviamo ora a vedere un caso in cui sia necessario stabilire l’associazione fra due variabili tramite l’indice V di Cramer. Stabiliamo due variabili, come ad esempio i due sessi (maschio e femmina) e la presenza o meno di dipendenza dall’alcol (si o no). A questo punto si può costruire una tabella di contingenza a doppia entrata in cui riportare le frequenze osservate per le quattro categorie individuate dall’associazione fra le variabili.
A questo punto si devono considerare le frequenze attese, ossia i numeri che ci si aspetterebbe in caso le due variabili fossero in rapporto di indipendenza. Ricavarle è semplice, basta fare ad esempio il prodotto fra i maschi fumatori per il totale degli uomini e delle donne fumatrici per il totale delle donne, dividendo poi i risultati ottenuti per la numerosità campionaria.
Più i valori delle due tabelle (frequenze osservate e attese) risulteranno simili minore sarà il grado di associazione che ricaverà dall’indice V di Cramer. Qualora invece questi risultino molto diversi potrò presumere una certa dipendenza fra le variabili scelte, in questo caso sesso e dipendenza dall’alcol.
Una volta ricavato il chi-quadrato utilizzando un software di statistica come R si può passare a sostituire nella formula vista prima i valori della tabella. Quindi righe (r) e colonne (c) diminuite di una unità, insieme al numero di osservazioni totali che andrà al posto di n. A questo punto in base al valore di V che otteniamo possiamo stabilire il grado di associazione. Più è grande maggiore sarà la dipendenza fra le due.
Interpretare l’indice V di Cramer
Come accennato questa misura può variare fra un valore minimo pari a 0 e uno massimo che è uguale a 1. Tuttavia per capire quanto forza risulti l’associazione fra le variabili occorre considerare anche il numero di gradi di libertà, che si ricavano da min[(n -1),(c – 1)]. Nel caso in cui ci sia un solo grado di libertà ad esempio si può parlare di associazione alta se V è maggiore di 0,5. e bassa se inferiore a 0,1.
Man mano che il numero di gradi aumenta però sarà cessaria una soglia dell’indice V di Cramer sempre più bassa per parlare di dipendenza fra le variabili considerate. Già se salgono a due il valore di V è sufficiente che superi 0,35 per dedurre che c’è un alto indice di associazione, e medio se il valore è attorno a 0,21. Un salto notevole rispetto a un grado solo.
Nel momento in cui i gradi superano il tre allora si parla di V alto anche al di sotto di 0,3. Per esempio quando una delle variabili è il colore degli occhi e quindi i colori possibili sono diversi, o quando si considerano i voti ottenuti a un esame. Se si hanno 4 gradi di libertà l’associazione fra le variabili è stretta intorno allo 0,25, media quando è circa 0,15 e minima solo quando è prossimo allo zero (0,05).
I limiti di questa misura di associazione
Per definire piccolo un dataset basta che le osservazioni anche solo di uno dei gradi della variabile risultino pari o inferiori a 5. La cosa migliore se le altre frequenze sono tarate su campioni più numerosi conviene escludere la colonna o la riga basate su dati troppo esigui. In questo modo non si rischierà di inficiare l’intera analisi, anche se escluderà alcuni casi.