Il teorema di Erone in geometria
Quando si studiano i triangoli conoscere la formula di Erone può tornare utile in molti problemi che a prima vista possono sembrare irrisolvibili. Consente infatti di poter trovare la superficie di un triangolo avendo note solo le misure dei suoi lati, senza avere bisogno di conoscere quelle delle sue altezze.
La sua definizione è attribuita al matematico greco Erone di Alessandria, vissuto nel primo secolo d.C. Ebbe modo di studiare in modo approfondito il lavoro di Archimede e Pitagora e fu da qui che prese spunto per i propri studi. Oltre alla geometria si interessò anche alla Fisica eseguendo ricerche nel campo dell’ottica.
Qual è la formula di Erone
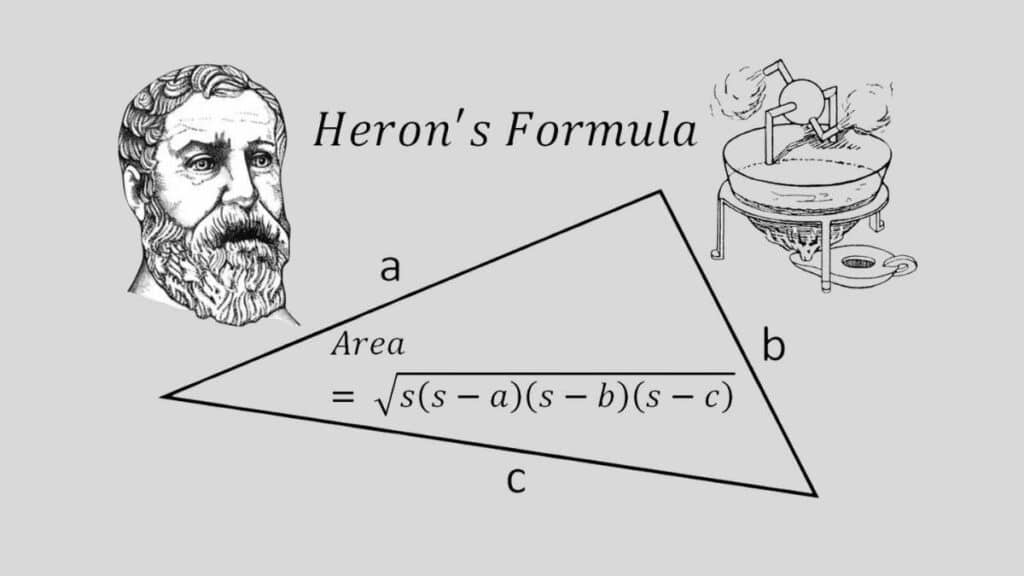
L’enunciato afferma che l’area di un triangolo è pari alla radice quadrata del suo semiperimetro moltiplicato fra le differenze tra questo e i tre lati della figura.
In un triangolo qualsiasi dove i lati siano a,b e c e il semiperimetro si indichi con p la formula si esprime quindi nella forma area = √p(p-a)(p-b)(p-c). Per calcolare il semiperimetro p basta fare (a + b + c)/2.
Vediamo allora un caso pratico dove si abbia un triangolo scaleno con i lati di misura pari a 23 cm, 15 cm e 12 cm. Per applicare la formula di Erone dobbiamo prima trovare il semiperimetro eseguendo la somma dei lati e poi dividendola per 2. Quindi (25 + 15 + 12)/2 = 52/2 = 26 cm. A questo punto non resta che sostituire i dati all’interno della formula.
Chiamiamo il lato maggiore a, quello intermedio b e quello più corto c. Per comodità possiamo calcolare le differenze prima di applicare la formula, quindi (p – a) = (26- 24) = 2 cm, poi (p – b) = (26 – 15) = 11 cm e infine (p – c) = 26 – 12 = 14 cm. A questo punto faremo area =√24(2)(11)(14) = √7.392 = 85,97 cm² .
Come si può notare Erone costituisce un’alternativa alla formula più classica che siamo abituati ad usare, ossia base x altezza/2. Tuttavia proprio perché torna utile solo nei casi in cui la misura dell’altezza non si può trovare e quindi di solito viene tenuta in secondo piano.
Che cosa sono i triangoli eroniani
Come per il teorema di Pitagora esistono le terne pitagoriche, così ci sono dei casi particolari per la formula di Erone.
Si definiscono eroniani i triangoli che come risultato del prodotto fra il semiperimetro e le singole differenze fra esso e i lati danno un quadrato perfetto. L’area quindi è una misura intera, non decimale o da approssimare.
Un esempio di triangolo eroniano è una figura con i lati di misure pari a 13 cm, 14 cm e 15 cm. Il suo semiperimetro p sarà uguale a (13 + 14+ 15)/2 = 42/2 = 21 cm e le differenze rispettivamente 8, 7 e 6 cm. Sostituendoli all’interno della formula vista prima allora avremo √21(8)(7)(6) = √7.056 = 84 cm². Un altro triangolo scaleno con misure eroniane ha i lati pari a 17, 25 e 26 cm.
Dato che come abbiamo detto la formula di Erone si può applicare a tutte le figure a tre lati esistono anche triangoli eroniani isosceli. Per esempio se le misure dei lati sono 6 cm per la base e 5 per i lati obliqui il risultato che si ottiene sotto radice è 144, il quadrato di 12. Infatti il semiperimetro è 8 e quindi √8(8 – 5)(8 – 5)(8 – 6).
Le terne pitagoriche sono a loro volta le misure dei lati dei triangoli eroniani. Basta provare con quella più nota (3,4,5) ed eseguire il calcolo. Il semiperimetro è 6, dunque sotto radice avremo 6 x (6 – 3)(6 – 4)(6 – 5) = 36, che è un quadrato perfetto (36).
Dimostrazione della formula di Erone
Esplicitando il prodotto notevole si ricava che l’incognita y è uguale a b2 +a2 – c2/2a. A questo punto si può sostituire questa forma nell’uguaglianza vista prima si ottiene h = √b2 – (b2 +a2 – c2/2a)2. Ora proviamo a sostituire questa forma ad h nella formula per il calcolo dell’area per ricavare la formula di Erone. Avremo A = [b x √b2 – (b2 +a2 – c2/2a)2]/2.
Portando anche b all’interno della radice la formula otterremo A = √a2b2/4 x (b2 +a2 – c2/2a)2/4. Semplificando si arriva a A = √[(a + b +c)/2)] [(a + b + c – 2c)/2] [(a + b + c – 2b)/2] [a + b + c – 2a)/2]. Se a + b + c/2 lo scriviamo come p otteniamo la formula vista prima.
I 12 grandi teoremi della matematica: il libro di William Dunham
La lista dei dodici grandi teoremi si trova nel suo libro Viaggio attraverso il genio e procede in ordine cronologico. Il primo teorema esaminato da Dunham è “la quadratura della lunula”, attribuito a Ippocrate di Chio.
Il quinto teorema descritto è quello della formula di Erone, dopodiché ci sono la soluzione dell’equazione cubica definita da Cardano e il calcolo del valore di π secondo Newton.