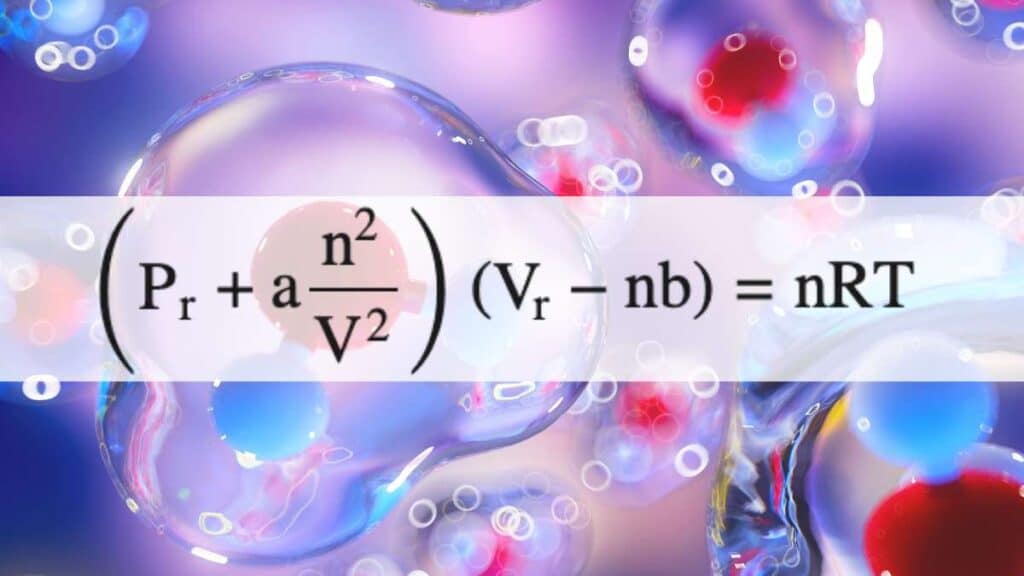Equazione di Van der Waals, l'equazione di stato che descrive il comportamento dei gas reali
Non si può parlare dell’equazione di Van der Waals senza prima riprendere quella che è l’equazione di stato dei gas perfetti. Infatti la funzione della formula che esamineremo in questo articolo è apportare delle correzioni a quest’ultima per applicarla ai gas reali, o meglio estenderla. Se usiamo solo PV = nRT utilizziamo un’approssimazione che non è applicabile alla realtà.
A definirla fu il fisico olandese Johannes Diderik van der Waals, una scoperta che gli fece ottenere il premio Nobel per la Fisica nel 1910. Il punto di svolta della formula fu comprendere che non era possibile trascurare la dimensione delle molecole di un gas né le forze intermolecolari. Non a caso definiamo anch’esse forze di Van der Waals.
La formula dell’equazione di Van der Waals
Come accennato questa equazione si applica ai gas reali e non ai gas perfetti. Rispetto all’equazione di stato introduce infatti due parametri in più. Questi corrispondono rispettivamente al volume occupato dalle molecole di gas e alle forze attrattive e repulsive che esistono fra di loro e ne influenzano il movimento.
Dopo questa introduzione vediamo di esaminare la formula. L’equazione di Van der Waals si scrive (P + an2/V2)(V – nb) = nRT. Al suo interno abbiamo:
- P è la pressione del gas.
- a è un parametro che serve determinare sperimentalmente per ogni gas reale considerato e serve a determinare gli urti delle molecole di gas contro la parete accostato al fattore n2/V2. Per il gas elio per esempio vale 0,034, mentre per l’ossigeno 1,39.
- n corrisponde al numero di moli di gas che stiamo considerando, V al volume che occupano.
- b è un altro parametro caratteristico per ogni sostanza gassosa e permette di capire lo spazio in cui le molecole del gas sono effettivamente libere di muoversi. Per l’elio vale 0,034, per l’ossigeno 0,032.
- R è la costante dei gas e il suo valore cambia rispetto alle unità di misura utilizzate per gli altri parametri. Se utilizziamo litri per il volume e atmosfere per la pressione allora equivale a 0,0821 atm x L/molK.
- T è la temperatura assoluta e si misura sempre in gradi Kelvin.
Le principali differenze fra gas ideali e gas reali
Vediamo di approfondire quali sono le caratteristiche di un gas perfetto. Dato che l’equazione di Van der Waals si applica alle sostanze gassose che troviamo in natura infatti non si può applicare a un contesto ideale. Tuttavia in termodinamica torna utile usare i gas perfetti per semplificare lo studio di vari fenomeni.
Il passaggio ai gas reali è più complesso, visto che occorre considerare le proprietà chimiche di ciascuno e non può esimersi da un controllo sperimentale. Un gas ideale è prima di tutto costituito da particelle puntiformi, di cui possiamo trascurare la massa. In più queste non hanno interazioni fra loro (sono non interagenti) e perciò non interferiscono con il moto reciproco.
Come vale per i gas reali secondo l’equazione di Van der Waals anche le molecole del gas ideale urtano le pareti del recipiente in cui si trovano. Tuttavia gli urti che effettuano sono perfettamente elastici, ovvero non le portano a perdere energia cinetica o quantità di moto. Per quanto riguarda il loro moto, questo è casuale e rivolto verso tutte le direzioni.
A essere pignoli dobbiamo dire che in particolari condizioni sperimentali le particelle di un gas reale si comportano in modo simile a quelle di uno ideale. Perché questo accada occorre portarlo ad alta temperatura e condizioni di bassa pressione. Diversamente, non si può usare l’equazione PV = nRT.
L’equazione di Van der Waals e le forze intermolecolari
Troviamo poi le forze di London, che al contrario delle precedenti si verificano tra molecole non polari. Tuttavia grazie al moto degli elettroni anche queste molecole possono diventare polari per brevi intervalli di tempo. Ossia nel momento in cui la nube elettronica è più concentrata su una zona specifica. Si crea quindi un dipolo istantaneo.
Possono essere della tipologia ione – dipolo indotto oppure dipolo – dipolo indotto. Solitamente le forze di van der Waals variano anche in base alle dimensioni delle molecole.