Circonferenza goniometrica: la guida completa con teoria e esercizi
Lo studio della trigonometria spaventa molti al terzo anno di superiori quando vedono la circonferenza goniometrica per la prima volta. Questo disegno è però fondamentale per iniziare a comprendere le funzioni goniometriche e i concetti di seno, coseno, tangente e cotangente.
Di per sé ricorda un po’ una torta una volta disegnati gli angoli principali, divisa in più fette come si usa per le frazioni alle elementari. La sua dimensione può variare a seconda dell’ampiezza dell’unità di misura ma qualunque sia la scala il suo raggio sugli assi cartesiani vale sempre 1. Vedremo di seguito perché.
Circonferenza goniometrica: formula e caratteristiche
Come ogni circonferenza anche questa è un luogo dei punti equidistanti da un centro che nello specifico coincide con l’origine degli assi cartesiani x e y. Ci troviamo infatti nel piano bidimensionale e il raggio del cerchio è sempre di misura uguale a uno, qualunque sia la grandezza dell’unità di misura scelta.
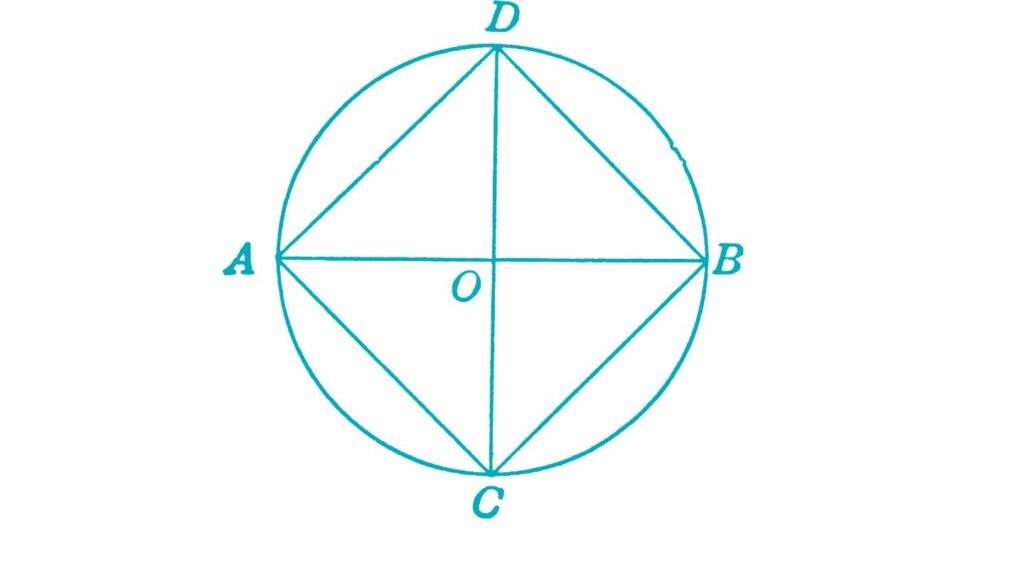
La circonferenza goniometrica quindi tocca gli assi in 4 punti diversi con le seguenti coordinate: A (1;0), B (-1;0), C (0; 1) e D (0; -1). Due sull’asse delle ascisse e due sull’asse delle ordinate. Indicarli è importante anche perché ogni arco compreso fra due di questi punti è un multiplo o un sottomultiplo di 90°, o meglio di π come vedremo in seguito.
La formula di questa curva è x2 + y2 = 1. Ogni punto P (xP; yP) preso sulla circonferenza se si traccia il raggio che lo unisce all’origine disegna un angolo compreso fra gli 0° e i 360°, di cui O costituisce il vertice. Per ciascun angolo α individuato si individua un triangolo rettangolo dove il raggio OP è l’ipotenusa. Invece la perpendicolare condotta da P all’asse e la proiezione del raggio sono i cateti.
La costruzione del triangolo è fondamentale per capire che cosa sono seno e coseno. Per ogni angolo con vertice in O infatti si definisce seno il rapporto fra la proiezione dell’ipotenusa e l’ipotenusa stessa, e coseno quello fra l’altro lato del triangolo e l’ipotenusa.
Come si suddivide in radianti
La misura di questa curva da formula canonica vale 2πr. Dato che il valore del raggio della circonferenza goniometrica è pari a 1 allora questa la formula si può scrivere direttamente come 2π. L’angolo giro che ha la stessa forma del cerchio vale 360°, quindi si può affermare tranquillamente che 360° = 2π.
La metà esatta e quindi un angolo piatto vale quindi 2π/2 = π (180°). Manca quindi solo l’angolo retto tra quelli con un valore fisso e che è a sua volta corrisponde a 180°/2, dunque π/2. Ci sono però anche altri sottomultipli che in trigonometria hanno rilievo ossia gli angoli di ampiezza pari a 30° (π/6), 45° (π/4) e 60° (π/3).
Per tutti gli angoli contenuti nella circonferenza goniometrica di ampiezze che sono multipli di quelli elencati c’è comunque un valore rapportato a quello di π. Ad esempio 270° è 3/2 π (π/2 x 3), 120° è 2/3 π (π/3 x 2) e 135° è 3/4 π (π/4 x 3). Se invece si immagina di fare più volte il giro completo della circonferenza si passa a 4π, 6π e così via.
In effetti disegnare un angolo su tale circonferenza equivale anche tutti quelli che hanno la stessa ampiezza ma hanno fatto un giro in più. Quindi ad esempio non si scrive solamente π/4 bensì π/4 + 2kπ. I valori di seno e coseno fra di loro rispettano la seguente relazione: sin2α + cos2α = 1.
Tangente e cotangente nella circonferenza goniometrica
Oltre al seno e al coseno ci sono altre due funzioni rilevanti che si individuano in trigonometria, ossia la tangente (tan) e la cotangente (cotan) di ogni angolo. Prima di tutto definiamo la tangente: si tratta della retta che incontra la circonferenza in un punto P (1;0) e il prolungamento di un lato dell’angolo. Vale a dire quello che ne definisce l’ampiezza.
Per calcolare la tangente a un qualsiasi angolo derivato dalla suddivisione della circonferenza goniometrica è necessario conoscerne i valori di seno e coseno. La formula da utilizzare infatti è tanα = sinα/cosα. Questo però vale solo se l’ampiezza dell’angolo è diversa da 90° o 270°, che hanno coseno pari a zero.
La cotangente invece è la retta che a sua volta come la tangente incontra il prolungamento del secondo lato nell’angolo. La differenza sostanziale però è che non tocca la circonferenza nel punto (1;0) bensì nel punto C di coordinate (0;1). In sintesi la tangente tocca l’asse delle ascisse mentre la cotangente quello delle ordinate.
Per calcolare la cotangente la formula è molto simile a quella della tangente ed è facile confonderla perché si invertono semplicemente numeratore e denominatore. Ossia cotanα = cosα/sinα. L’unico caso in cui non vale è quello in cui l’ampiezza dell’angolo sia pari a 180°, caso in cui il seno ha valore nullo.
I valori più ricorrenti da imparare
- Per π e 2π abbiamo cos= 1 e sin = 0. Invece per l’angolo di 90° (π/2) è esattamente il contrario, ossia cos= 0 e sin = 1. Infine i 270° (3/2π) invece cos= 0 e sin = -1.
- L’angolo di 45° (π/4) ha coseno e seno uguali, che valgono √2/2. L’angolo di 135° (3/4π) ha coseno negativo, 5/4π ha entrambi negativi e infine 7/4π ha solo il seno negativo.
- Gli angoli di 60° (π/3) e di 30° (π/6) concludono la lista dei valori da imparare per la circonferenza goniometrica. Il primo ha cos =1/2 e sin = √3/2. Invece l’angolo di 30° è l’opposto, con cos = √3/2 e sin = 1/2.