Analisi armonica: il teorema di Fourier
Quando parliamo del teorema di Fourier ci addentriamo in una branca della Matematica nota come analisi armonica. Nel dettaglio questa materia studia la rappresentazione delle funzioni e dei segnali sotto forma di andamenti ondulatori periodici (le armoniche). Pur trattandosi di un principio di per sé teorico lo si può applicare anche in Fisica, per esempio in Acustica quando si affrontano le onde sonore.
Un’onda si definisce armonica quando la sua legge di vibrazione è di tipo sinusoidale, per cui le si definisce anche sinusoidi. Armoniche o sinusoidi costituiscono un sottoinsieme all’interno del gruppo delle onde periodiche. Si contraddistinguono per avere variazioni che si ripetono a distanza di un determinato intervallo di tempo, il periodo.
L’enunciato del teorema di Fourier
Definito da Jean Baptiste Joseph Fourier a inizio ‘800 questo teorema prende in considerazione una funzione o un segnale periodico di periodo T0 o frequenza f0 = 1/T0 continua e limitata. L’enunciato afferma che tale funzione si può rappresentare con una somma di funzioni sinusoidali pure, di ampiezza e frequenza multiple della frequenza fondamentale f0.
Esiste anche un’espressione matematica per rappresentare questa relazione, chiamata sviluppo in serie di Fourier. Per definirla la pulsazione che genera il segnale si indica con 0 = 2
f0. Il segnale/funzione periodica si indica con v(t) o f(t), e lo sviluppo in serie così diventa v(t) = A0 + A1sin(ωt +ϕ1) + A2sin(2 ωt +ϕ2) + A3sin(3ωt + ϕ3)…. Per semplificare possiamo anche scriverla come sommatoria, ossia ΣAnsin(ωt)cosϕn.
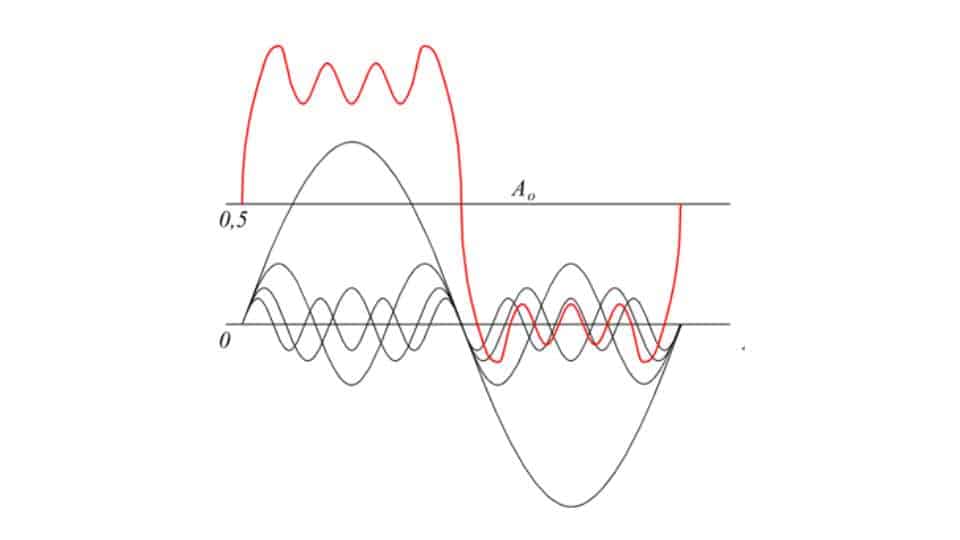
Il primo elemento A1sin(ωt +ϕ1) secondo il teorema di Fourier rappresenta l’armonica fondamentale. La seconda armonica ha frequenza doppia rispetto al segnale, la terza il triplo e si continua così, in quanto devono avere frequenze multiple di quella fondamentale. Ogni funzione o segnale sviluppabile secondo la serie di Fourier deve essere continua e sommabile nell’intervallo (0,T0), ovvero il suo integrale deve avere un valore finito.
Tutte le armoniche successive a quella fondamentale sono dette successive o parziali, e insieme costituiscono l’armonica complessa. Ma finora abbiamo visto solo formule, e usando questo teorema è possibile analizzare una qualsiasi onda periodica per determinarne le componenti armoniche.
Cosa sono gli spettrogrammi
Con il teorema di Fourier è possibile dare una rappresentazione sintetica delle funzioni periodiche all’interno di un sistema cartesiano detto dominio delle frequenze. Infatti definisce che le frequenze dello spettro di emissione hanno tutte valori multipli di quella fondamentale e non c’è bisogno di disegnare le varie oscillazioni ed è sufficiente costruire un grafico a barre.
Basta sistemare sull’asse delle ascisse le frequenze e su quello delle ordinate, riportare il valore della frequenza fondamentale e poi ricavare le altre. Supponiamo di avere lo sviluppo in serie di una funzione costituita dalla sovrapposizione di tre onde armoniche, con ampiezza di 1,2 3 cm e frequenze di 600,400 e 200 Hz. La frequenza dell’armonica fondamentale (f0) è la più bassa, quindi quella di frequenza 200 Hz.
Da questa armonica complessa vedo che come descritto dal teorema di Fourier le due successive hanno frequenze multiple di 200 (400 e 600). Otterrò allora un grafico del dominio delle frequenze con tre barre. Sull’asse delle y vedrò i valori 1, 2 e 3, mentre su quello delle x le frequenze 200, 400 e 600. Ma come fare qualora tra le armoniche che si sovrappongono non si trovi un valore che divide gli altri (es. frequenza 300, 400 e 600)?
In simili casi possiamo suppore che si tratta dello sviluppo in serie dove l’armonica fondamentale risultava di 100 Hz. Poi però stata soppressa sia questa che la seconda e la quinta armonica parziale. Nel grafico di conseguenza le tre barre non saranno alla stessa distanza fra di loro, ma le prime due vicine e la terza più distante.
Il teorema di Fourier e il principio di sovrapposizione
Definiamo principio di sovrapposizione l’enunciato che segue. Se due o più onde della stessa natura che si propagano all’interno dello stesso mezzo si sovrappongono in un punto la perturbazione è la somma algebrica delle oscillazione di ogni singola onda. Questa legge spiega perché quando suona una band o un’orchestra i suoni si sentono distintamente fra di loro.
Anche il teorema di Fourier vede le onde armoniche come il risultato della sovrapposizione di altre armoniche più semplici, dunque è facile dedurne il principio di sovrapposizione. Lo si può scrivere anche nella forma in cui date due onde y1(x,t) e y2(x,t) la loro sovrapposizione y(x,t)= y1(x,t)+ y2(x,t). risulterà un’onda a sua volta. La questione però cambia se ci sono due onde con la stessa frequenza anziché averne due che sono multipli fra di loro.
Quando si verifica questo caso siamo fuori da quanto stabilito dal teorema di Fourier perché si verifica un’interferenza. Questa può essere di due tipologie:
- Interferenza costruttiva. In questo caso le due onde hanno ampiezza uguale e frequenza in concordanza di fase, ovvero oscillazioni dove le creste sembrano sovrapponibili. Il risultato sarà un’armonica con onde di ampiezza pari al doppio di quella delle onde originarie.
- Interferenza distruttiva. Si tratta della condizione in cui le due onde di partenza hanno comunque ampiezza e frequenza coincidenti ma risultano in opposizione di fase con le loro oscillazioni. Il risultato è che la somma algebrica si compensa e ne deriva un’onda nulla.