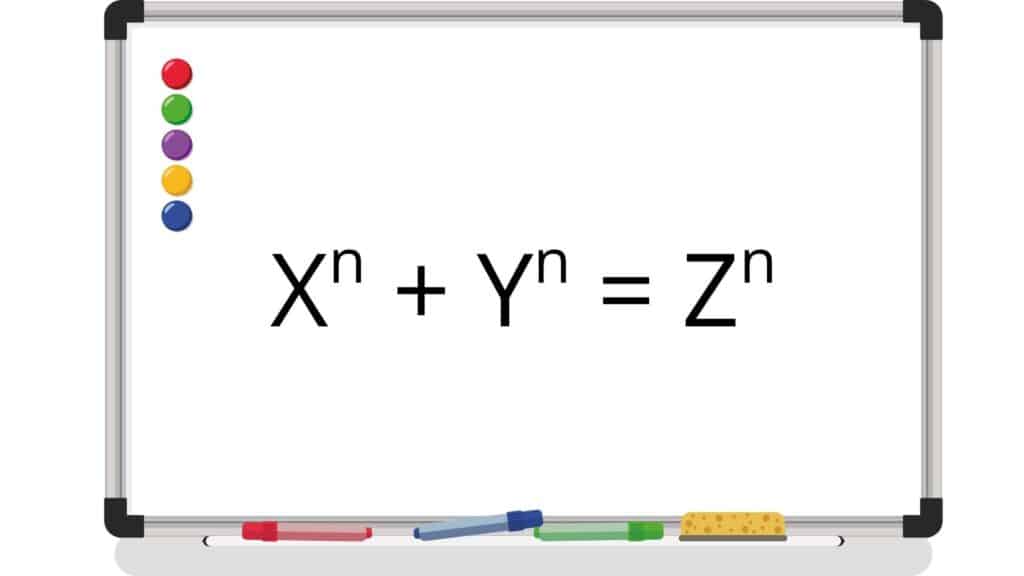Teorema di Fermat per la determinazione dei punti stazionari
Quando si analizza una funzione matematica il teorema di Fermat torna utile per determinare quelli che definiamo i suoi punti stazionari. Si indicano così quei punti in cui la retta tangente al grafico della funzione risulta parallela all’asse delle ascisse. Perché questo accada in ogni punto stazionario la derivata prima della funzione si annulla.
Più spesso sui libri di Matematica si utilizza un’altra definizione, ovvero punti critici. Ne fanno parte i punti di massimo e di minimo, ovvero i valori più alti e più bassi che tale funzione assume all’interno del suo dominio. In più questa categoria comprende anche i punti di flesso, dove si verifica un cambiamento nella curvatura del grafico.
L’enunciato del teorema di Fermat
Il testo del teorema per le derivate afferma quanto segue, considerando una funzione f(x) definita all’interno di un intervallo fra due valori distinti a e b. Se nell’intervallo [a,b] ha un punto di massimo o minimo relativo nel punto x0 allora la derivata prima della funzione in quel punto è nulla. In formula possiamo scrivere f’(x0) = 0. Definiamo meglio cosa si intende per massimo o minimo relativo.
Per riconoscere un minimo relativo la derivata sinistra della funzione nel punto è minore di zero mentre la derivata destra è maggiore di zero. Nel caso del punto di massimo relativo vale esattamente il contrario. Il teorema di Fermat ha tuttavia un limite, in quanto il punto x0 non può coincidere con uno degli estremi dell’intervallo (a o b) ma deve per forza essere interno.
Possiamo riscrivere il teorema anche in un’altra forma. Vale a dire dicendo che il fatto che la derivata prima si annulli nel punto x0 è la condizione necessaria perché questo sia un punto di massimo o minimo relativo. Infatti se la derivata prima f'(x) risulta diversa da zero in un punto allora questo non risulta estremante. Allo stesso tempo non possiamo affermare nulla con certezza sul punto considerato.
Si può perciò dire che conoscere questa regola matematica rappresenta un aiuto considerevole per identificare i punti stazionari in un grafico. Tuttavia non è l’unico sistema per trovarli e può far correre il rischio di non individuarne qualcuno. Alcuni punti estremanti non si possono individuare usando solo questo metodo.
La dimostrazione matematica
Dopo aver visto l’enunciato è ora di dimostrare quanto afferma il teorema di Fermat. Considerando sempre un punto x0 di una funzione f(x) che è anche un punto di massimo allora per un valore molto piccolo non definito h possiamo dire che f(x0 + h) ≤ f(x0). Allora spostando a sinistra il membro a destra del simbolo otteniamo f(x0 + h) – f(x0)≤ 0.
Consideriamo ora i due casi in cui h sia positivo o negativo. Nel primo il punto (x0 + h) è a destra rispetto a x0. Possiamo allora dividere tutto per h e lasciare invariato il simbolo ≤ e ottenere la derivata destra dalla formula f’ + (x0) ≤ 0. Se invece h ha valore negativo dividere l’espressione per h richiede di cambiare il verso e scrivere f(x0 + h) – f(x0)/h ≥ 0. E la derivata sinistra sarà f’ – (x0)≥ 0.
Poiché la funzione è derivabile nel punto x0 allora derivata destra e sinistra saranno uguali. Vediamo allora che il teorema di Fermat vale perché otteniamo f’ + (x0) = f’ – (x0) e spostiamo a sinistra la parte a destra avremo f’ + (x0) – f’ – (x0) = 0 e f’(x0) = 0. Questo è infatti l’unico valore comune fra le due derivate.
La dimostrazione si può fare anche considerando x0 come un punto di minimo. della funzione, arrivando comunque al medesimo risultato ma con le derivate destra e sinistra invertite fra di loro.
La storia di Pierre de Fermat
Non pubblicò quasi nulla di ciò che scoprì e la maggior parte dei risultati che ottenne sono rimasti all’interno di carteggi scambiati con dei matematici dell’epoca. Spedì infatti diverse lettere a Blaise Pascal, insieme al quale gettò le basi per il calcolo delle probabilità. Si dedicò anche alla teoria dei numeri e alle basi della geometria analitica.
Anche se finora abbiamo parlato di teorema di Fermat in realtà ne esiste più di uno oltre a quello relativo ai punti stazionari. Il più famoso è noto come “l’ultimo” e rimase senza dimostrazione per secoli dato che Pierre de Fermat non la rese mai nota anche se affermò di averla scritta. Alla fine ci riuscì Andrew Wiles nel 1994 e da allora il suo nome fu aggiunto alla denominazione di questo problema matematico.
La formula di questo “ultimo teorema” è an + bn = cn. L’affermazione di Pierre de Fermat è che non esistano soluzioni reali per questa equazione se n risulta maggiore di 2. Per decenni si riuscì a dimostrare questo enunciato solo per valori singoli di n, non per l’intervallo dato. Eulero per esempio ci riuscì solo per n = 3.