La tautologia nella logica formale
In logica esiste una particolare forma di enunciato definita tautologia, un termine di origine greca. Deriva dall’unione delle parole ταὐτό, che significa “stesso”, e λογία, che vuol dire “discorso”. Oltre che in questa branca della Matematica troviamo questo termine anche in linguistica, dove indica invece una figura retorica. In questo caso assume il significato di affermazione ridondante.
Nell’ambito logico possiamo definirla come un enunciato che si giudica vero per definizione, e che in un discorso non fornisce informazioni di rilievo perché risaputa. Per comprendere a fondo questo concetto di seguito non solo lo analizzeremo a fondo ma vedremo qualche esempio che lo renderà più tangibile.
La tautologia nelle tavole di verità
Prima di tutto non si tratta di un enunciato semplice, ma composto da almeno due frasi. Si possono quindi escludere tutte le proposizioni a sé stanti, anche se è possibile unirne due per dare vita a un’affermazione di questo tipo. Abbiamo già anticipato che la si giudica vera per definizione, e il suo opposto, ovvero un enunciato falso in ogni caso, è la contraddizione.
Dato che siamo in ambito logico bisogna inquadrare come si presenta questo enunciato all’interno delle tavole di verità. Prendiamo due proposizioni singole, che indicheremo con le lettere s e t. Possiamo scrivere allora (s ˄ t) => s. Vediamo perciò che si mette una congiunzione, indicata dal simbolo ‘˄‘, che indica l’unione delle due proposizioni formando la tautologia.
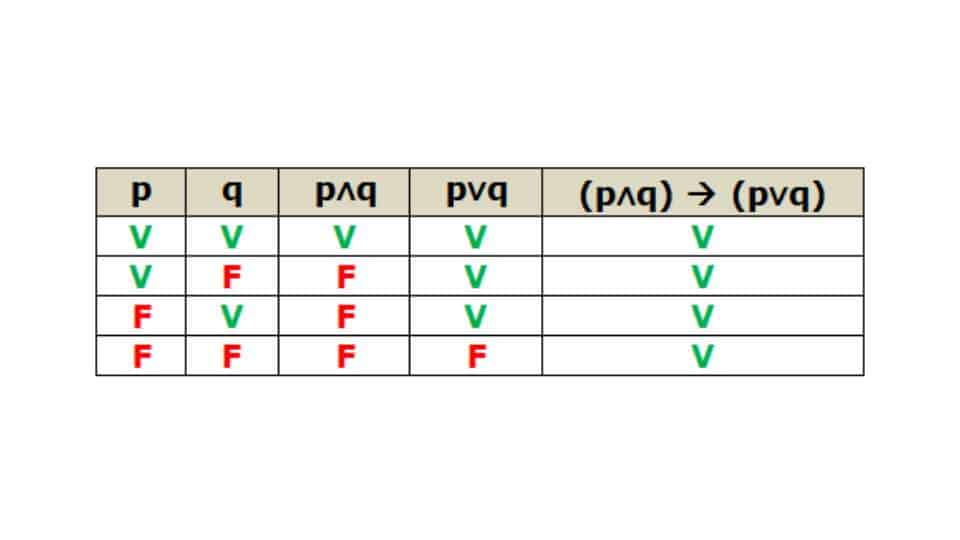
La freccia invece indica un’implicazione, dove ciò che si trova a sinistra della freccia forma l’antecedente e ciò che sta a destra invece il conseguente. Nella tabella di verità da costruire mettiamo tutte le combinazioni possibili, a partire da quella in cui s e t sono vere a quella in cui sono entrambe false e i casi in cui solo s o t risulta vera.
Una volta compilata la tabella inserendo i valori di verità per (s ˄ t ) arriviamo alla colonna finale, dove inseriamo vero o falso per (s ˄ t) => s. Qui però si otterrà che per qualsiasi coppia di valori, da (V,V) a (F,F), l’enunciato che risulta sarà sempre vero. Questa però è solo una possibile forma, perché ne esistono molte altre.
Qualche esempio pratico
Per capire bene quando si sia di fronte o meno a una tautologia è meglio vedere almeno un paio di questi enunciati scritti per esteso. Un esempio classico è la frase “o c’è il sole o non c’è“. Contiene due proposizioni, e copre tutte le possibilità metereologiche in poche parole. Poiché non è possibile escludere nessuna delle due frasi allora la loro unione risulta vera a prescindere.
Una volta capito questo concetto diventa facile crearne altre, e realizzare quanto queste affermazioni risultino ridondanti se ascoltate con attenzione. Possiamo per esempio dire “sono sempre felice, tranne quando non lo sono” e lo stesso esempio si può replicare inserendo una qualsiasi altra emozione al posto della felicità, come la tristezza o la rabbia.
Estendo un enunciato che si presenta come tautologia possiamo trasformarlo in un’argomentazione, che però a sua volta risulterà vuota e ripetitiva. Eppure capita di pronunciarne all’interno di un discorso comune senza accorgersene, soprattutto se non si ha molto da dire. Per esempio dire “è così perché deve essere così“, oppure “sono d’accordo perché sono sono della stessa opinione“.
In sintesi potremmo dire che la tautologia pur essendo sempre vera non dice nulla di effettivo e pare soltanto ribadire qualcosa che pare ovvio. Un’argomentazione di tipo tautologico può dilatarsi per righe o pagine, ma giunti alla fine si avrà l’impressione di non sapere nulla di nuovo rispetto a prima sul tema trattato.
La tautologia nel caso del modus ponens e del modus tollens
Si tratta di una deduzione ricavata da due proposizioni logiche e da un’implicazione. Date le proposizioni q e r possiamo scrivere[(q => r) ˄ q] => r. Per fare un esempio pratico potremmo stabilire che q è “oggi c’è il sole” e r invece è “il sentiero è asciutto“.
Potremmo tradurre la formula nel modo che segue. Se q che implica r è un enunciato vero, e la proposizione q è vera, allora anche r di conseguenza lo sarà. Nella tabella di verità che si va a costruire ci saranno cinque colonne: le prima due occupate da q e r, nella terza q => r, nella quarta[(q => r) ˄ q] e nell’ultima lo schema completo.
Una volta compilata la tabella si nota che si ottiene il valore “V” per tutte le possibili combinazioni. Il modus ponens risulta quindi a sua volta una forma di tautologia. Passiamo ora al modus tollens, altra forma di ragionamento comune dove si afferma che se q che implica r è vero e così anche la negazione di r, allora anche la negazione di q risulterà vera.
In simboli possiamo allora scrivere [(q => r) ˄ ¬r] => ¬q. Il simbolo ¬ indica la negazione, ovvero l’opposto di ciò che afferma la proposizione. Anche in questo caso costruendo la tabella osserviamo che il modus tollens risulta sempre vero.