I concetto della resistività elettrica: la seconda legge di Ohm
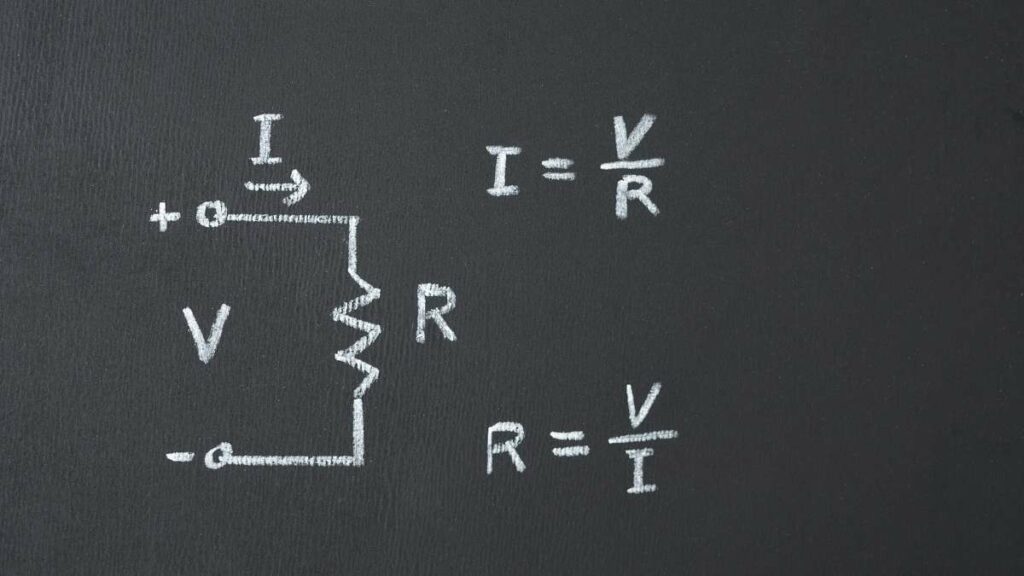
La prima e la seconda legge di Ohm sono enunciati fondamentali per comprendere il funzionamento dei circuiti elettrici, dai più semplici ai più articolati. Mentre la prima definisce la relazione che intercorre fra la differenza di potenziale (ΔV) e l’intensità di corrente (i) quella che indagheremo definisce il concetto della resistività elettrica (ρ).
A questo proposito meglio ricordare che la resistività e la resistenza elettrica sono grandezze molto diverse fra loro. La prima infatti indica una proprietà che dipende dalla tipologia di materiale di cui è fatto un conduttore. La seconda invece si concentra sul rapporto che lega la resistenza di un conduttore alle sue dimensioni.
Enunciato e formula della seconda legge di Ohm
Questa regola definisce come si comporta un elemento in grado di condurre la corrente elettrica in un circuito e afferma quanto segue.
La resistenza di un conduttore è direttamente proporzionale alla sua lunghezza e inversamente proporzionale alla superficie della sua sezione trasversale.
In formula si scrive R = ρ l/S, in cui:
- R è la resistenza, ossia la tendenza da parte di un corpo a contrastare il passaggio della corrente quando è sottoposto a una tensione elettrica.
- ρ è la resistività, chiamata anche resistenza elettrica specifica perché si tratta di una proprietà che dipende dal tipo di materiale conduttore. La sua unità di misura è l’Ohm per metro (Ω·m) e si tara su un metro cubo di materiale.
- S, che di solito sta per superficie, nella seconda legge di Ohm indica l’area della sezione trasversale. Vale a dire il conduttore tagliato con direzione perpendicolare alla sua lunghezza. Di conseguenza il taglio è ortogonale anche al flusso della corrente elettrica.
- l è la lunghezza del conduttore, ossia la sua dimensione più sviluppata.
Un esempio pratico
Ora che abbiamo visto la formula della seconda legge di Ohm nel dettaglio possiamo provare ad applicarla a un caso tangibile.
Supponiamo di avere un cilindro di materiale conduttore (rame) di altezza pari a 1 metro. Gli si applica una tensione di 5 V e si fa circolare una corrente di intensità pari a 0,08 Ampère (A). Qual è il raggio del cilindro? (ρ = 1,7 x x 10-8 Ω·m)
Tenendo presente la formula R = ρ l/S dati del problema ci forniscono il valore di l e di ρ.Tuttavia dobbiamo trovare il modo di ricavarci R e S per risolvere il problema. Infatti per trovare il raggio dobbiamo partire dall’area trasversale, che rappresenta anche la base del cilindro. Trovare R è facile ricordando la prima legge di Ohm e la sua formula, ossia V = R x i.
Abbiamo già il valore di V quindi è sufficiente ricavare la formula inversa, che è R = V/i. Sostituendo i dati del problema troviamo perciò che R è uguale a 5 V/0,08A = 62,5 Ω. Ora abbiamo tutte le grandezze richieste dalla formula della seconda legge di Ohm quindi possiamo ricavare l’area della sezione trasversale con la formula inversa S = (ρ x l)/R.
Sostituendo i valori trovati otteniamo S = (1,7 x x 10-8 Ω·m) x 1 m/62,5 Ω = 2,72 x 10-10 m2 . Poiché abbiamo un conduttore cilindrico la superficie trovata è quella di un cerchio. La formula dell’area del cerchio è πr² quindi basta dividere per π e fare la radice quadrata del risultato. r = √S/π = 9,3 x 10-6 m.
La resistività e le sue implicazioni nella seconda legge di Ohm
Questa grandezza non serve solo a calcolare la resistenza di un conduttore in un circuito. Infatti anche solo dal suo valore, scevro da altre implicazioni, possiamo capire se ci troviamo di fronte a un isolante, un semiconduttore o un materiale che conduce bene la corrente elettrica. Questa ultima categoria si suddivide in conduttori e superconduttori.
Partiamo dagli isolanti, ovvero i corpi che si contrastano il passaggio della corrente elettrica. Nel loro caso il valore di ρ ha un valore che supera i 1 x 1010 Ω⋅m come per esempio lo zolfo (S) che ha 1×10 15 Ω⋅m. Uno dei valori più alti che possiamo registrare lo ha il teflon ( fino 10 24 Ω⋅m), un materiale plastico che si usa per rendere antiaderenti i tegami.
Arriviamo al caso di interesse, ossia i conduttori. Il loro valore di resistività varia fra un minimo di 1×10 -6 e un massimo 1 x 10-8 Ω⋅m. In questa categoria rientra la maggior parte dei metalli (argento, rame, oro, titanio…). Infine abbiamo i superconduttori, materiali che al di sotto di una determinata temperatura presentano resistività nulla (ρ = 0).
Un esperimento semplice nei laboratori delle scuole
Replicarlo richiede di costruire un semplice circuito elettrico composto da un filo di lega di rame e nichel (costantina), collegato a un generatore con dei cavi di rame. Serve anche munirsi di un amperometro, un voltimetro e un metro.
Questi strumenti misurano rispettivamente l’intensità di corrente, la differenza di potenziale e la lunghezza del conduttore.
L’esperimento consiste nel ricavare la misure di R (usando la prima legge) variando la lunghezza del filo di costantina ma senza mutare la differenza di potenziale.
Dopodiché si possono ripetere le misurazioni ma procurandosi fili di costantina di lunghezza uguale ma spessore diverso. In tal caso si considera come varia la resistenza in funzione della sezione trasversale. Dai valori si può osservare se la resistenza aumenta o diminuisce i funzione del variare di l e di S.