Il principio di Pascal e la meccanica dei fluidi
Alla base della meccanica dei fluidi c’è il principio di Pascal, enunciato dall’omonimo matematico e fisico francese che la enunciò nel trattato Sur l’equilibre des liqueurs. Pubblicato nel 1653, riportava i risultati di un esperimento svolto circa sei anni prima usando due semplici oggetti: una botte e un tubo di metallo. Oggi ricordiamo questo esperimento come La botte di Pascal.
La legge definita da questo scienziato è alla base del funzionamento di svariati attrezzi. Prima di tutto il torchio idraulico che è il caso pratico più comune presentato nei problemi, il sifone e i freni idraulici che troviamo nei veicoli a motore. Anche gli schemi acquedottistici la sfruttano per mantenere una determinata pressione all’interno delle condutture.
Il principio di Pascal e l’esperimento da cui nasce
La sua dimostrazione pratica avvenne nel 1647, quando Blaise Pascal decise di effettuare un esperimento sfruttando una botte di legno, un tubo di metallo e dell’acqua. Una volta inserito il tubo nella botte attraverso un foro largo quanto il suo diametro sulla base superiore iniziò a versare il liquido un po’ alla volta. Dopo un po’ la botte si ruppe a causa della pressione dell’acqua premeva sulle sue pareti.
La botte si spaccava senza che si creasse una sola crepa ma come se fosse scoppiato qualcosa all’interno. Come afferma il principio di Pascal quindi la pressione era uguale su ogni punto della superficie interna e non concentrata sul fondo. La dimostrazione però si può anche replicare “in piccolo” senza usare una botte ma con una semplice bottiglia di plastica piena d’acqua.
Sistemando la bottiglia piena al centro di una bacinella basta prendere un ago spesso e praticare dei piccoli fori lungo tutto il bordo. Da ciascuno di questi partirà un piccolo zampillo d’acqua, ma indipendentemente dal punto in cui è stato praticato il foro l’intensità del getto sarà uguale. Questo perché anche qui la pressione del liquido è uguale in tutti i punti della superficie.
Il legame con la legge di Stevino
Il principio di Pascal non è esprimibile con una formula perché esprime quella che è una proprietà intrinseca dei fluidi. Tuttavia spesso la si associa alla legge di Stevino, un’equazione fondamentale per lo studio dell’idrostatica. La sua funzione è quella di stabilire la pressione esercitata da un fluido su un corpo immerso a una data profondità.
La formula di Stevino per calcolare la pressione man mano che si scende in profondità in un fluido è p = ρgh. Nel dettaglio ρ indica la densità del fluido e varia a seconda della sua natura, g è l’accelerazione di gravità (9,81 m/s2) e h la profondità a cui ci si trova, espressa in metri. Tuttavia su ogni fluido grava una pressione aggiuntiva, ovvero quella atmosferica (patm) equivalente a 1 bar.
Di conseguenza bisogna riscrivere la formula precedente nel formato p = patm + ρgh. Secondo il principio di Pascal esercitando una pressione su un fluido questa si trasmette uguale in qualsiasi suo punto, perciò dovremo considerare patm sia sulla superficie che sul fondo di un lago o di un oceano. Sul nostro pianeta vale 1 bar, ma se fossimo su Nettuno questa sarebbe diversa dato che l’atmosfera ha una composizione diversa.
Considerare la pressione atmosferica nella legge di Stevino è dunque una conseguenza di quanto dimostrato da Blaise Pascal. Per chi pratica immersioni e nella progettazione di batiscafi e sottomarini è fondamentale tenerne conto per regolare la pressurizzazione interna oltre che la resistenza degli scafi.
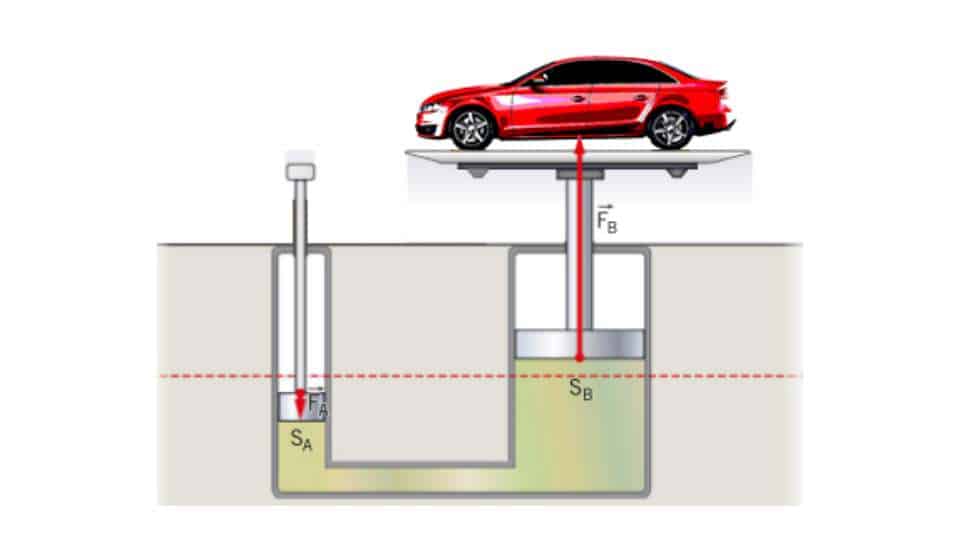
Il principio di Pascal e il torchio idraulico
Il funzionamento del torchio idraulico è molto semplice. Si esercita una forza sul pistone con la sezione minore creandone una maggiore che consente di sollevare l’altro. La forza (F1) esercitata su S1 è direzionata verso il basso, mentre quella (F2) su S2 verso l’alto. Dividendo F1 e F2 per le rispettivi superfici dei pistoni troviamo p1 e p2, e secondo il principio di Pascal le due pressioni si equivalgono (p1 = p2).
Possiamo perciò scrivere che F1/ S1 = F2/ S2. Dato che forza e superficie sono inversamente proporzionali più si ampia la sezione S2 minore sarà la forza F1 da applicare per sollevare il pistone con il carico. Nella maggior parte dei casi le sezioni S1 e S2 sono circolari quindi basta conoscere il loro raggio per ricavarle.