Numeri primi: cosa sono e le loro caratteristiche

Cosa sono i numeri primi

I numeri primi sono alla base delle teorie matematiche e sono numeri interi positivi che possono essere divisi soltanto per sé stessi e per 1. Proprio per questo motivo si parla di numeri con soltanto due divisori distinti.

In secondo luogo è necessario che sia sempre maggiore di 1. I numeri che hanno più di due divisori vengono invece definiti composti. Tutti i numeri primi sono dispari ad eccezione del 2, che è anche quello più piccolo della serie. Infatti tutti i numeri pari successivi si possono dividere per 2. La serie è 2, 3, 5, 7, 11, 13, 17, 19 per poi continuare in una successione infinita.

Quali sono le caratteristiche dei numeri primi

In passato il numero 1 era inserito all’interno della sequenza, tanto che nel 1914 Derrick Norman Lehmer lo incluse nella sua tavola numerica. Al giorno d’oggi la sua esclusione viene accettata per evitare di dover riformulare diversi teoremi in modo più complesso per far fronte alle variazioni che si originerebbero. Esiste una modalità specifica, chiamata il test di primalità, per verificare se si ha a che fare con un numero primo. Basta accertarsi che non possa essere diviso per nessun numero primo inferiore. Un altra soluzione riguarda il cosiddetto setaccio di Eratostene, un algoritmo che consente di evitare le divisioni. In definitiva permette di ottenere la sequenza dei numeri primi uguali oppure minori rispetto all’elemento usato come riferimento.

Come Riconoscere i Numeri Primi

Riconoscere un numero primo da uno composito può essere un compito impegnativo, ma ci sono alcune strategie che possono semplificare il processo.

1. Test di Divisione

Il metodo più semplice per verificare se un numero è primo è il “test di divisione”. Per determinare se un numero è primo, è sufficiente provare a dividerlo per tutti i numeri compresi tra 2 e la radice quadrata del numero stesso. Se nessuno di questi numeri è un divisore esatto, allora il numero è primo. Questo perché, se ci fosse un divisore maggiore della radice quadrata del numero, dovrebbe esserci anche un divisore minore, e quindi il numero sarebbe composto.

2. Test di Wilson

Il “test di Wilson” è un metodo più avanzato per verificare se un numero è primo. Questo test sfrutta il fatto che un numero primo p soddisfa l’equazione:

(p – 1)! ≡ -1 (mod p)

Dove “!” rappresenta il fattoriale di un numero. Se l’equazione è vera per un certo numero p, allora p è primo. Tuttavia, questo test è più complesso da eseguire rispetto al test di divisione e può richiedere più calcoli.

3. Test di primalità probabilistico

Esistono anche algoritmi di test di primalità probabilistici, come il test di Miller-Rabin, che possono fornire una probabilità molto alta che un numero sia primo. Questi algoritmi sono spesso utilizzati in applicazioni crittografiche e possono essere molto veloci per numeri grandi.

Le applicazioni dei numeri primi

Il concetto di numero primo è uno dei principi fondamentali dello studio matematico dei numeri interi, indicato con il nome di teoria dei numeri. Infatti la loro moltiplicazione consente di ottenere tutti gli altri numeri interi. Al tempo stesso la loro serie è infinita. Proprio per questi motivi i numeri primi sono stati oggetto di numerosi studi fin dall’epoca degli antichi Greci. Non bisogna dimenticare che all’interno degli scritti di Euclide vi sono teoremi grazi ai quali poterli calcolare in una successione di elementi fino a 120. Inoltre sono basilari per:

• diverse branche della matematica pura, come la geometria e l’algebra;
• teoremi non ancora dimostrabili, come la congettura di Goldbach, l’ipotesi di Riemann e la congettura dei primi gemelli;
• la crittografia e la matematica applicata.

Perché il numero 1 non è considerato un numero primo?

Nel mondo affascinante della teoria dei numeri, esiste una domanda intrigante: è il numero 1 un numero primo?

La risposta a questa domanda potrebbe sorprendervi, poiché la convenzione matematica comune esclude il numero 1 dall’insieme dei numeri primi. In questo articolo, esploreremo i motivi di questa esclusione e perché il numero 1 non gode dello stesso status degli altri numeri primi.

Il Requisito dei Due Divisori

Una delle caratteristiche distintive dei numeri primi è che ogni numero primo ha esattamente due divisori distinti: 1 e se stesso. Questa definizione è fondamentale nella teoria dei numeri, ed è ciò che differenzia i numeri primi dagli altri numeri naturali. Tuttavia, il numero 1 non soddisfa questa regola.

Il numero 1 ha un solo divisore, ovvero se stesso. Questo contrasta con i numeri primi, che hanno sempre due divisori. Questa differenza è fondamentale, poiché gran parte della teoria dei numeri si basa su questa proprietà.

Complicazioni nelle Formule e nei Teoremi

L’inclusione del numero 1 tra i numeri primi comporterebbe complicazioni significative nelle formule e nei teoremi matematici.
Ad esempio, consideriamo la funzione φ di Eulero, che è definita come la cardinalità dell’insieme degli interi compresi tra 0 e n, tali che il massimo comune tra a e n sia uguale a 1 [(a, n) = 1].

Se il numero 1 fosse considerato primo, dovremmo stabilire due formule diverse per φ: una per 1 e un’altra per i numeri primi p ≥ 2. Questo renderebbe le definizioni e le dimostrazioni matematiche molto più complesse e meno eleganti.

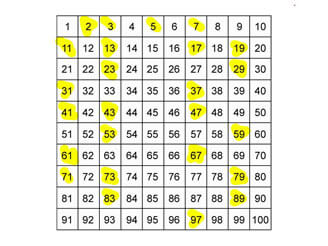
Il crivello di Eratostene

Un esempio concreto che illustra le complicazioni che deriverebbero dall’inclusione del numero 1 tra i numeri primi è il crivello di Eratostene.
Questo metodo sarebbe profondamente influenzato, cancellando tutti i numeri tranne 1 al primo passo se il numero 1 fosse considerato primo. Questo renderebbe il crivello inutile per identificare altri numeri primi.

Funzione Ω e altri contesti matematici

In vari contesti matematici, come la funzione Ω che conta il numero di fattori primi di un numero, l’inclusione del numero 1 porterebbe a problemi e ambiguità.
Si potrebbe ottenere una serie di valori indefiniti per la funzione Ω se il 1 fosse considerato primo, poiché si potrebbe includere una potenza α arbitraria di 1 nella fattorizzazione di un numero.

In definitiva, sebbene a prima vista potrebbe sembrare naturale considerare il numero 1 come un numero primo, la teoria dei numeri e la matematica in generale preferiscono escluderlo.
Questa esclusione semplifica notevolmente le definizioni, i teoremi e gli algoritmi matematici. In matematica, l’utilità e la versatilità delle definizioni vengono spesso determinate dalla loro capacità di semplificare il lavoro e di evitare eccezioni complesse. Quindi, mentre il numero 1 è un numero speciale, non è considerato un numero primo per motivi fondamentali nella teoria dei numeri.

I numeri primi sono uno degli aspetti più affascinanti della teoria dei numeri, e il loro riconoscimento è una parte importante della matematica. Mentre ci sono metodi per riconoscere i numeri primi, il processo può diventare complesso per numeri molto grandi. Tuttavia, grazie a algoritmi avanzati e software specializzato, possiamo identificare i numeri primi con precisione e utilizzarli in una varietà di applicazioni pratiche, dalla crittografia alla ricerca scientifica.