Moto del proiettile o moto parabolico
In Fisica il moto parabolico per dinamica si nota subito che descrive quella che è la traiettoria che compie il lancio di una palla di cannone dal basso verso l’alto. Questa tipologia di movimento deriva dalla combinazione del moto rettilineo uniforme e di quello uniformemente accelerato. La condizione in cui avviene prevede che i due vettori risultino perpendicolari fra di loro.
Gli oggetti che compiono traiettorie paraboliche di conseguenza sono considerati proiettili, quindi si parla spesso anche di moto del proiettile. Come sempre in Fisica non si tratta di una rappresentazione del tutto accurata della realtà perché trascura l’effetto che l’aria ha sull’oggetto in movimento.
Il moto proiettile: definizione e legge oraria
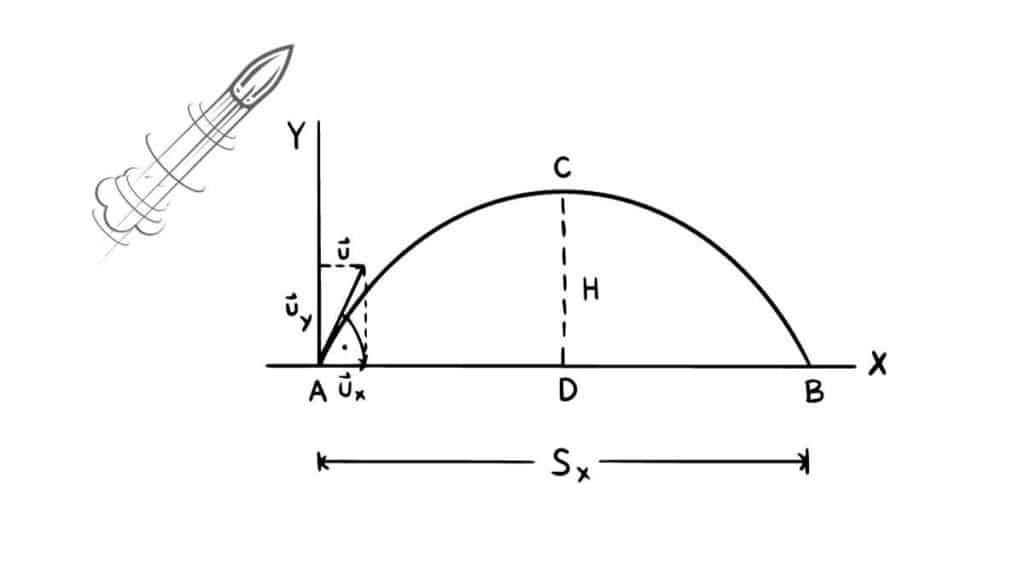
Per iniziare a studiare il moto parabolico prima di tutto capire che cosa si intende con questa espressione. Per definizione si tratta dello spostamento di un corpo o punto materiale che si muove lungo una traiettoria parabolica ed è soggetto alla forza di gravità. In un sistema di riferimento cartesiano dove sia disegnata la parabola distinguo due componenti del moto lungo gli assi x e y.
Come accennato il moto del proiettile è l’unione di due tipi di movimento. Lungo l’asse delle ascisse (X) il corpo si sposta di moto rettilineo uniforme, mentre lungo quello delle ordinate (Y) secondo quello uniformemente accelerato. La parabola ha un’inclinazione pari a un angolo che si indica con α compreso fra 0 e 90°.
La velocità iniziale del corpo si indica con v0 di cui si distinguono una componente orizzontale (v0x = v0cosaα) e una verticale (v0y= v0senα). Il moto parabolico ha una legge oraria a sua volta suddivisa in base alle due componenti del movimento. Lungo l’asse x la legge oraria è x = x0 + v0xt dove x0 è il punto di partenza.
Lungo l’asse y invece la formula è y = -1/2gt2 + v0yt + y0. Con y0 si indica la quota massima che il corpo raggiunge durante la traiettoria parabolica. Si distinguono però più casi a seconda che l’oggetto sia lanciato con velocità orizzontale o velocità qualunque.
Il moto parabolico di un proiettile lanciato con velocità qualunque
Un caso esemplare è un oggetto lanciato da un edificio alto, come una torre o un grattacielo. Dato che si parte da una quota definita la sia indica con h all’interno delle formule. In questo caso le due componenti del moto avranno per l’asse delle ascisse x = v0t mentre per l’asse delle ordinate y = -1/2gt2 + h.
Per ottenere l’equazione della traiettoria di questo moto proiettile basta eliminare l’incognita del tempo. Per farlo è sufficiente ricavarlo dalla prima equazione e quindi invece che t scrivere x/v0. A questo punto la seconda equazione diventerà y = -1/2g(x/v0)2 + h. poi semplificata in y = -1/2g/v02x2 + h.
Per fare un esempio vediamo il caso in cui dalla cima di una torre alta 30 m un ragazzo getta una palla di gomma. Il lancio avviene con velocità orizzontale pari a 14 m/s. Come consegna si richiede di scrivere le equazioni del moto parabolico della palla oltre a quella della traiettoria.
Sostituendo i dati del problema nelle formule si ottiene quanto segue. Poiché v0 =14 m/s quindi x = 14t e y =-1/2gt2 + 30. Per l’equazione della traiettoria come visto prima si sostituisce a t il rapporto x/v0. Da qui deriva y = -1/2(9,8/142)x2 + 30 = -0,109x2 + 30.
Il moto proiettile lanciato con velocità qualsiasi
In questo caso il lancio dell’oggetto avviene da terra, descrivendo una parabola che parte da un punto con y = 0. Per studiare il movimento in questo caso serve conoscere sia la velocità iniziale che l’angolazione con cui un corpo viene lanciato. Si tratta del caso del cannone che spara un proiettile verso un bersaglio.
Le formule che si usano quindi considerato seno e coseno dell’angolo per le due componenti verticale e orizzontale. Quindi x = v0xt e y = v0yt – 1/2gt2. Ma per capire meglio vediamo un esempio di caso pratico con un esercizio semplice. Da terra sparo un proiettile da un cannone con velocità pari a 250 m/s e un angolo α rispetto al terreno pari a 45°. Trova le due componenti della velocità.
Per trovare v0x serve fare il prodotto fra la velocità iniziale dell’oggetto che compie il moto parabolico e il coseno dell’angolo. Dato che in questo caso cosα = √2/2 allora si fa 250 x √2/2 = 176 m/s. Mentre v0y si calcola moltiplicando senα per v0, ma dato che il valore è uguale al coseno anche il risultato sarà identico.
L’equazione della traiettoria come nel caso precedente prevede di sostituire a t il rapporto x/v0. Così si ottiene y = (v0y/v0)x – (g/v0x2)x2.
La storia della balistica e dello studio del moto parabolico
- Teoria aristotelica. Il proiettile sparato seguiva inizialmente una traiettoria orizzontale per poi cadere verticalmente verso il basso per effetto del peso. In questo caso la palla di cannone avrebbe seguito un percorso a L.
- Teoria dell’impeto. L’azione esercitata dal peso del proiettile che lo attira verso il basso inizia da subito. Questo fenomeno porta il corpo ad incurvare la traiettoria già mentre sta salendo di quota e quindi a compiere un moto parabolico. Questa teoria poi analizzata da Galileo era sostenuta tra gli altri anche da Leonardo da Vinci.