Le leggi di De Morgan e la teoria degli insiemi
Definite da un matematico britannico vissuto nel 1800, le leggi di De Morgan sono fondamentali per affrontare lo studio della teoria degli insiemi. Augustus De Morgan si dedicò anche all’algebra relazionale, ma proprio questi teoremi sono considerati il suo contributo principale. Tornano infatti molto utili per l’analisi e la costruzione dei sistemi logici informatici.
Si tratta di due teoremi rilevanti in quanto consentono di svolgere operazioni fra gli insiemi e quindi di metterli in relazioni fra di loro. Sono regole molto semplici e intuitive soprattutto se rappresentante utilizzando i diagrammi di Eulero Venn. Le operazioni che entrano in gioco in particolare sono l’intersezione, l’unione e la costruzione dell’insieme complementare.
La prima delle leggi di De Morgan
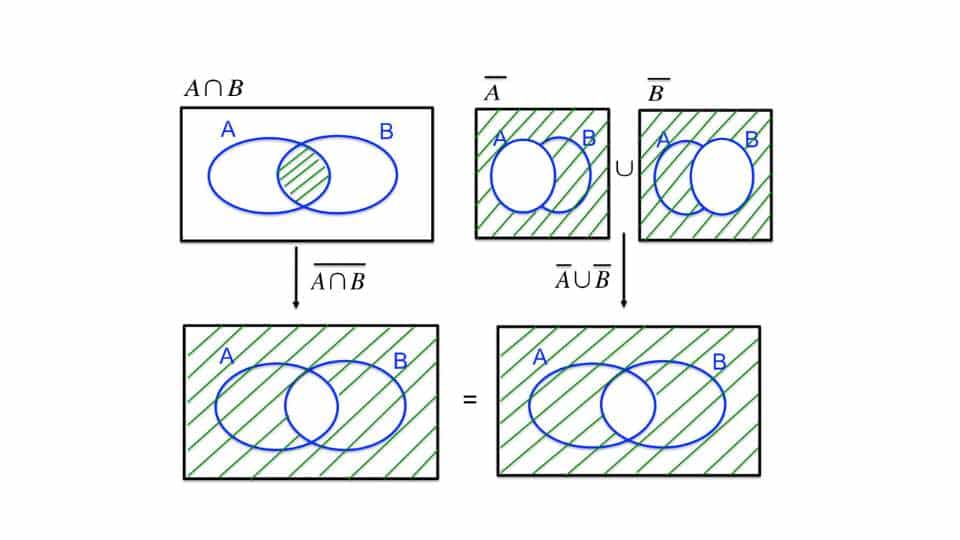
Iniziamo con quello che è riconosciuto come il primo dei due teoremi e che permette di definire il complementare dell’intersezione fra due insiemi. Il suo enunciato afferma che esso è pari all’unione fra il complementare del primo insieme e il complementare del secondo. Il complementare di un insieme contenuto in un altro sono tutti gli elementi di quello esterno che non appartengono al sottoinsieme.
In formula possiamo scrivere questa legge come (A ∩ B)C = AC U BC. Considerando sia A che B come sottoinsiemi di un altro insieme U (universo), rappresentare la relazione con i diagrammi di Eulero Venn è semplice. Basta escludere l’intersezione fra A e B e considerare tutto il resto. Questa formula si può dimostrare sia quando A e B sono sottoinsiemi propri di un insieme U che quando risultano impropri.
Per rappresentare la prima delle leggi di De Morgan si ricorre di solito all’esempio dove sia effettivamente presente un’intersezione non vuota fra gli insiemi. Definendo A = {1,2,4,5,8}, B = {2,3,4,5,6,7} e U = {1,2,3,4,5,6,7,8,9,11,12} immaginiamo di dover trovare appunto (A ∩ B)C. Usando la formula possiamo trovare AC = {3,6,7,9,11,12} e BC = {1,8,9,11,12}.
Ora che abbiamo i complementari di entrambi gli insiemi possiamo effettuare la loro unione, che perciò sarà AC U BC = {1,3,6,7,8,9,11,12}. Vediamo che si tratta di tutti gli elementi presenti negli insiemi A, B e U ad esclusione di quelli interni all’intersezione fra A e B.
Il secondo teorema e il complementare dell’unione
Passiamo ora alla seconda delle leggi di De Morgan, che descrive come ricavare il complementare dell’unione di due insiemi invece che quello dell’intersezione. Il suo enunciato afferma che dati due insiemi A e B sottoinsiemi di U il complementare della loro unione è uguale all’intersezione fra il complementare di A e quello di B.
Il complementare di un qualsiasi insieme si può scrivere anche come insieme negato. Scriveremo allora la formula (A U B)C = AC∩ BC. Se la si vuole rappresentare con i diagrammi di Eulero Venn servirà disegnare l’insieme universo intorno ad A e B, che formano un’intersezione. La parte individuata dalla formula risulterà quella esterna ad A e B, interna al contorno di U.
Vediamo così che entrambe le leggi di De Morgan prevedono un’intersezione e un’unione, che con le formule viste diventano interscambiabili fra di loro. Proviamo come prima a fare un esempio, definendo A = {a,b,d,f,g}, B = {b,c,d,e,f,h,i} e U = {a,b,c,d,e,f,g,h,i,j,k}. A questo punto ci serve trovare AC = {c,e,h,i,j,k} e BC = {a,g,j,k}. Facendo la loro intersezione otterremo che AC∩ BC = {j,k}.
facendo il disegno vediamo appunto che i due elementi dell’intersezione fra i complementari risultano i soli esterni agli insiemi A e B.
Applicazioni delle leggi di De Morgan
Oltre che in insiemistica, questi due teoremi possono tornare utili nel calcolo delle probabilità. Per esempio quando si considerano eventi che sono indipendenti fra di loro usare queste formule e usare i loro complementari aiuta a semplificare i calcoli. Più interessante ancora è il loro utilizzo in ambito informatico. Spiegano infatti il legame fra i connettivi logici AND (intersezione) e OR (unione).
Questi infatti si trasformano nel proprio opposto quando c’è una negazione distribuita fra i membri interni a una parentesi o se la si raccoglie fuori. In informatica la negazione si identifica con il connettivo logico NOT. Volendo possiamo anche riscrivere le formule viste prima usando NOT, AND e OR invece dei simboli di operazioni fra gli insiemi.
Nel caso della prima delle leggi di De Morgani dobbiamo sostituire a complementare il connettore NOT, l’intersezione con AND. e l’unione con OR. Dunque avremo al posto di (A ∩ B)C = AC U BC la formula NOT(A AND B) = (NOT A) OR (NOT B). Per quanto riguarda il secondo teorema invece al posto della formula (A U B)C = AC∩ BC avremo NOT(A OR B) = (NOT A) AND (NOT B).
Anche nel campo della logica questi teoremi tornano utili per dimostrare l’equivalenza di espressioni logiche che paiono differenti e permettono di semplificare alcune dimostrazioni.