La legge di Stevino in idrostatica
Quando in Fisica ci si approccia alla branca dell’idrostatica ci si imbatte presto nella legge di Stevino. Si tratta di un enunciato che vanta una storia lunga quasi 500 anni dato che deve il suo nome a Simone Stevin, uno scienziato vissuto a cavallo fra il 1500 e il 1600. Lavorò in particolare come ingegnere idraulico nella Repubblica delle Sette Province Unite.
Oltre a definire questo principio che usiamo ancora oggi per capire la pressione esercitata dai liquidi Stevin fu anche un importante matematico. Ideò un metodo di notazione per i numeri decimali rendendo più facile svolgere le operazioni che li prevedevano. In più effettuò studi in ambito meccanico e architettonico.
Cosa afferma la legge di Stevino
Si tratta di un principio che vale per i fluidi incomprimibili, ovvero i liquidi.
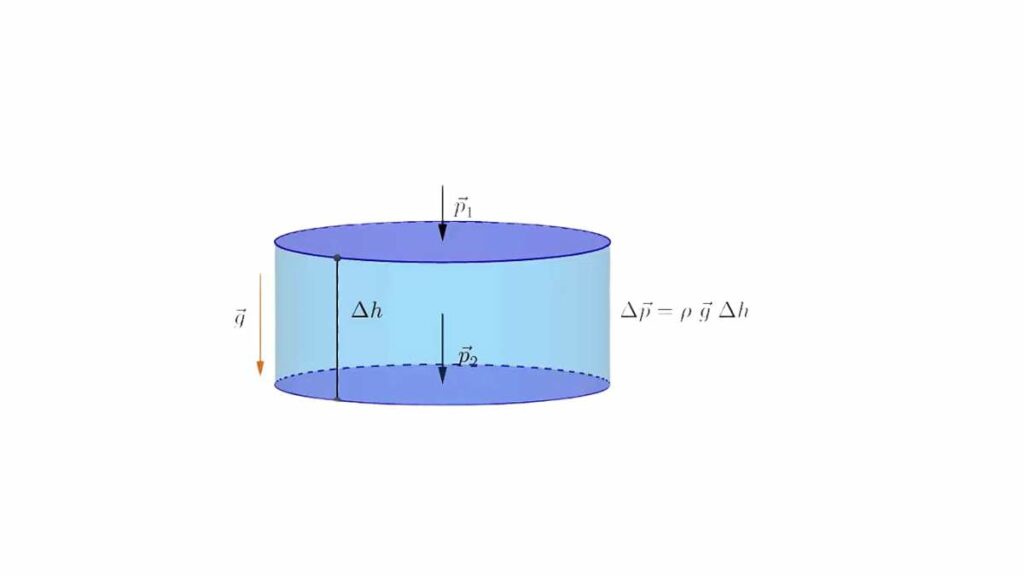
Il suo enunciato afferma che un fluido ideale in quiete è in grado di esercitare pressione su un corpo in base alla profondità a cui questo si trova. Al variare di questa quindi anche la pressione cambia, immaginando che il corpo si muova lungo una colonna d’acqua.
Quando si parla di fluido ideale si intende che al suo interno le uniche forza che si possono esercitare sono di tipo pressorio. Espressa come formula la legge di Stevino diventa P = ρgh o volendo essere più precisi visto che si parla di variazioni ΔP = ρgΔh. Per la precisione all’interno di questa equazione:
- h rappresenta la profondità a cui si trova il corpo considerato (e Δh la sua variazione). Si esprime in metri.
- g è l’accelerazione di gravità e il suo valore è 9,81 m/s². Anche mentre è immerso nel fluido infatti ogni corpo è comunque soggetto a questa forza che lo attira verso il basso.
- ρ è la densità del fluido. Quella dell’acqua distillata è pari a 1000 kg/m³. e quella dell’oceano di 1030 kg/m³. Dato che indichiamo la profondità in metri non usiamo più i grammi/cm³ ma ci rapportiamo ai metri cubi. Più è denso il liquido maggiore sarà la pressione che esercita.
Calcolare la pressione subacquea
Uno degli utilizzi pratici più importanti della legge di Stevino è quello di usarla per capire come prepararsi alle immersioni.
Chiunque abbia mai fatto un corso da sub sa bene che la pressione a cui si è soggetti aumenta man mano che si va in profondità. E in base a questa si capisce come effettuare la decompressione prima di risalire in superficie.
Quando si va sotto acqua prima di tutto bisogna ricordarsi che sopra di noi rimane la pressione atmosferica, pari a 101.325 Pascal (Pa). Ad ogni profondità quindi al valore trovato dalla formula vista prima occorre sempre sommare anche quella dell’aria esterna che preme sul fluido. Immaginiamo ora di immergerci con le bombole a 20 metri sotto il livello del mare.
La profondità (h) la abbiamo, la densità dell’acqua salata sappiamo già che è 1030 kg/m³ e il valore di g è sempre di 9,81 m/s². Usiamo allora la formula della legge di Stevino per trovare la pressione facendo 20 m x 9,81 m/s² x 1030 kg/m³ = 202086 kg/ ms² (Pa). Vediamo che si tratta di un valore che è circa il doppio della pressione dell’aria esterna.
Di conseguenza possiamo ricavare che ogni 10 metri di profondità la pressione su un corpo immerso aumenta di un valore quasi uguale alla pressione atmosferica. Grazie a questa approssimazione si possono effettuare immersioni in sicurezza anche a decine di metri sotto la superficie, risalendo con delle soste programmate.
Esercizi sulla legge di Stevino
A questo punto possiamo ricavare la densità dalla formula inversa ρ =ΔP/Δhg. Di conseguenza 50.675/9,81 x 1,2 = 4.304 kg/m³. Passiamo adesso a un esercizio classico, quello dei sottomarini. Abbiamo un mezzo subacqueo che sta viaggiando a 3, 2 km di profondità sotto la superficie. A quale pressione è sottoposto?
Come già detto la densità dell’oceano è di 1030 kg/m³, ma dobbiamo convertire la profondità in metri per procedere (3,2 km = 3.200 metri). A questo punto possiamo calcolare la pressione esercitata dalla colonna d’acqua facendo 1030 x 3.200 x 9,81 = 32.333.760 Pascal (3,23 x 107 Pa). Bisogna inoltre sommare quella atmosferica, che porta il totale a 3,24 x 107.