Cosa misura il coefficiente statistico Indice di Gini
Il coefficiente statistico noto come indice di Gini deve il suo nome all’economista italiano Corrado Gini, fondatore dell‘Istituto Nazionale di Statistica (Istat). Nella sua attività di ricerca applicò le analisi statistiche in modo interdisciplinare, dagli studi di Biologia all’Economia e all’Antropologia. Il suo indice tuttavia è il motivo che gli valse più fama in assoluto.
L’utilizzo di questo coefficiente è essenziale ancora oggi per misurare la diseguaglianza di una distribuzione statistica. Trova applicazione ad esempio per stimare come sia distribuita la ricchezza all’interno della popolazione di un paese. Dunque può portare alla luce quando presenti grosse differenze di reddito all’interno di uno stato o di una regione.
Come interpretare l’indice di Gini
I valori di questo coefficiente sono sempre compresi nell’intervallo fra 0 e 1.
Se è pari a zero la concentrazione è nulla e dunque il parametro che si sta indagando risulta equidistribuito all’interno della popolazione in esame. Invece se ha valore 1 indica che la concentrazione è massima e le disuguaglianze di distribuzione del parametro sono notevoli.
Possiamo suddividere la scala di valori in quattro scaglioni. Dato che l’indice di Gini si rappresenta con il simbolo G possiamo indicare la prima fascia come quella in cui 0 ≤ G < 0,25. Si tratta dell’intervallo in cui la dispersione è bassa, mentre a partire da 0,25 e fino a 0,5 allora G indica una diseguaglianza medio-bassa.
La terza fascia di valori è 0,5 ≤ G < 0,75, e corrisponde alla dispersione medio-alta, e infine quando G supera il valore di 0,75 diventa alta. Per rappresentare graficamente questo coefficiente nella valutazioni del reddito si ricorre a un cartogramma. Vale a dire una carta geografica dove tramite i colori si rappresentano i valori di un determinato fenomeno.
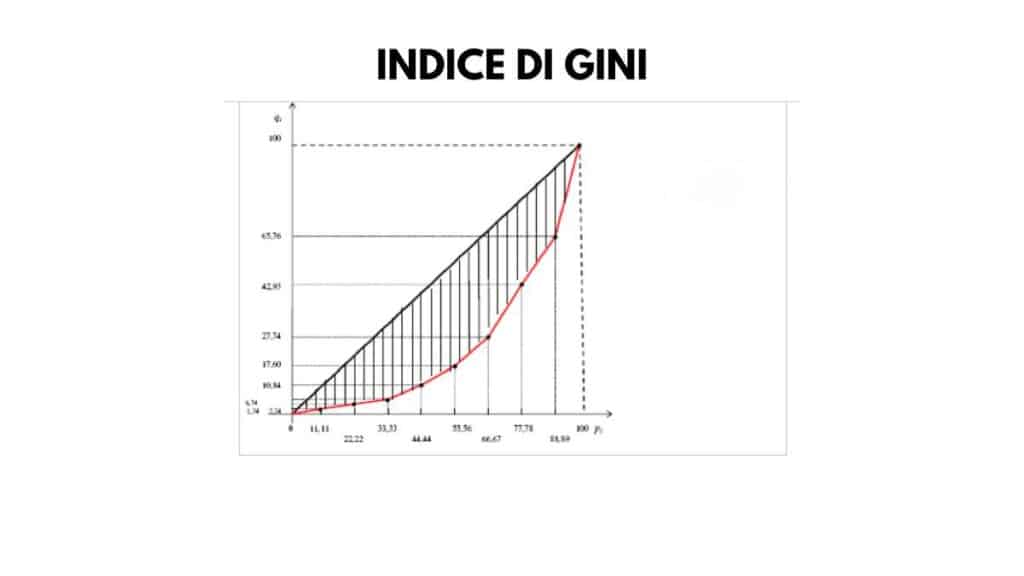
In alternativa, se si rappresentano i valori del parametro che si misura usando la curva di Lorenz, occorre tracciare la retta di perfetta uguaglianza. Per ricavare il coefficiente da questo grafico dobbiamo ora evidenziare l’area compresa fra questa linea e quella della curva. G infatti è il rapporto tra l’area individuata dalla retta e quella del grafico di Lorenz.
Come si calcola il coefficiente per i redditi
Quando si vuole ricavare il grado di diseguaglianza della distribuzione della ricchezza bisogna prima di tutto definire quali siano le classi di reddito. Tali classi xi avranno ciascuna una frequenza assoluta associata ni, (vale a dire la numerosità della popolazione che appartiene a tale fascia di reddito). Moltiplicando xi per l’ni associato si ottengono le intensità assolute (ii).
A questo punto ci occorrono le frequenze relative (pi) e le intensità relative (qi). Calcolare le prime richiede di dividere le frequenze ni per la numerosità totale della popolazione (N), mentre per trovare le seconde serve dividere le intensità assolute ii per quella totale I. Infine dobbiamo ottenere frequenze relative cumulate (Pi) e intensità relative cumulate (Qi).
A questo punto possiamo usare la formula per ricavare l’indice di Gini. Questa richiede la differenza fra 1 e il rapporto fra la sommatoria delle differenze fra i valori di Pi e Qi e la sommatoria di Pi. Possiamo perciò scrivere il calcolo nella forma G = Σn-1(Pi-Qi)/Σn-1Pi. Esiste anche un’altra formula più semplice, ossia G = 1 – 2 x (Σn-1Qi)/n – 1. Usando Pi e Qi inoltre è possibile costruire la curva di Lorenz accennata prima.
Il motivo per cui questo grafico risulta associato al coefficiente G è che l’economista che lo sviluppò aveva a sua volta l’intento di mostrare le disparità di reddito presenti nel suo paese. Corrado Gini se ne servì a sua volta per illustrare il valore dei suoi studi, e forse grazie a questa scelta presto divenne noto anche negli Stati Uniti.
Le proprietà dell’indice di Gini
In particolare l’indice di Gini diminuirà nel caso sopra citato grazie alla redistribuzione della ricchezza che consegue al passaggio di denaro. Se il trasferimento avviene in senso contrario invece aumenterà la disparità fra le classi di reddito e anche G avrà un valore più alto. Anche le trasformazioni di scala dei redditi possono influenzarlo, ad esempio quando gli stipendi delle diverse classi raddoppiano o si dimezzano.
Una situazione in cui G può risultare un indicatore fuorviante è il confronto fra stati diversi, anche se simili dal punto di vista dello stipendio medio. Se la superficie geografica fra i due risulta molto diversa infatti i valori del coefficiente possono risultare inutili per un confronto oggettivo, per esempio fra Austria e Norvegia. I paesi più estesi tendono ad avere un valore di G più alto di quelli più piccoli. In più anche i sistemi di retribuzione possono variare fra i paesi.
Bisogna anche considerare l’accuratezza dei dati utilizzati per calcolare il coefficiente. Questa dipende sia dalla numerosità del campione che dal sistema di raccolta delle informazioni, perché non si possono escludere errori. Pare anche che G tenda a oscillare di più quando si presentano variazioni del reddito della classe media rispetto a quelle agli estremi della scala.