Logica matematica: capire le condizioni necessarie e sufficienti nella
In Matematica, e soprattutto quando si studia la branca della Logica, è importante capire cosa siano le condizioni necessarie e sufficienti. Si tratta di concetti che a prima vista possono sembrare complessi ma in realtà si possono applicare anche in situazioni quotidiane e non si tratta solo di immagini astratte.
Prima di tutto parlando di “condizione” si intende qualcosa di necessario, un requisito che va soddisfatto perché qualcosa avvenga o meno. I termini “necessaria” e “sufficiente” però vanno approfonditi perché danno una sfumatura diversa al nome che accompagnano.
Definizione di condizioni necessarie e sufficienti
Per capire di che si tratta occorre fare un piccolo passo indietro e partire dalle basi della Logica. In Matematica infatti esistono due tipi di condizione, le necessarie (indicate con CN) e le sufficienti (abbreviate in CS). Nel caso delle CN, si tratta del caso in cui un evento sia soggetto al possesso di un requisito, che però da solo non basta a farlo accadere o a dimostrare un fatto come vero.
Per quanto riguarda le condizioni sufficienti invece si tratta di una situazione che può determinare da sola il verificarsi di un evento o di un fatto. Unendo queste due definizioni, le condizioni necessarie e sufficienti sono dei requisiti che se soddisfatti garantiscono che un evento accada. Se invece non sono verificati allora è sicuro che questo non avverrà. Si indicano con CNS.
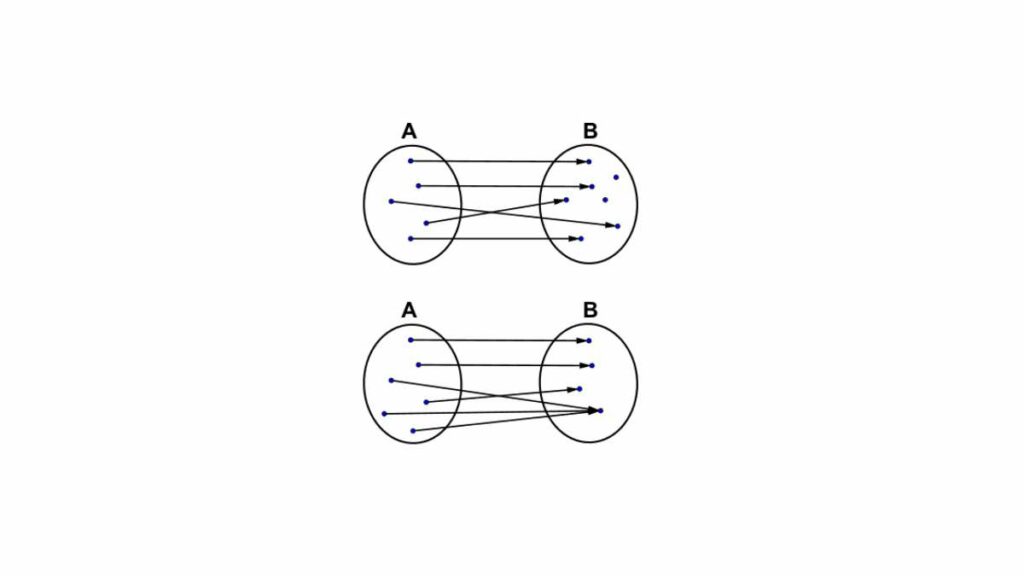
Solitamente le condizioni si scrivono come proposizioni che descrivono brevemente la qualità o la situazione di cui si sta parlando. In logica per non dover scrivere l’intera frase si attribuisce loro una lettera maiuscola. Per stabilire invece quale sia la relazione che lega due proposizioni si utilizzano le frecce unidirezionali (=> ) o bidirezionali (<=>)a seconda di quale essa sia.
Ogni condizione, sia che si tratti di una CN, una CS o una CNS, se messa per iscritto inizia sempre con la particella “Se”. Quindi se scrivo “Se una persona è disoccupata allora non lavora” ho due proposizioni di cui “se una persona è disoccupata” è la condizione e “non lavora” è l’evento a lei legato. Si tratta di una CNS quindi scriverò che A <=> B.
Le differenze fra “necessaria” e “non necessaria” in Logica
Per comprendere meglio cosa siano le condizioni necessarie e sufficienti bisogna prima approfondire questi due concetti in forma separata. Come “necessario” si intende un requisito che se vero (V) comporta il verificarsi di un evento, mentre se falso (F) impedisce che questo accada. Per esempio “Se vuoi prendere la laurea, devi frequentare l’università”.
Se invece la condizione non è necessaria invece le sue implicazioni sono l’esatto opposto. Se è vera l’evento si verifica, mentre in caso sia falsa questo può avvenire oppure no. La sua natura infatti non ha modo di influenzarlo come invece avviene per i requisiti necessari. Un esempio è “Se un numero è divisibile per 4 allora un numero è pari”.
Queste due proposizioni infatti fra di loro sono in una relazione che non richiede per forza che la prima sia vera. Per esempio il numero 30 è pari, ma se si prova a dividerlo per 4 il risultato è un numero decimale (30 : 4 = 7,5). Questo perché essere divisibile per 4 è sufficiente perché un numero sia pari, ma non indispensabile (o meglio necessario).
Differenza fra “sufficiente” e “non sufficiente” in Logica
Quando invece una proposizione enuncia una condizione non sufficiente perché un evento si verifichi allora il fatto che sia vera o falsa non ha rilevanza. Una condizione di questo tipo non può avere impatto e anzi risulta slegata dalla circostanza che potrebbe o meno verificarsi. Per questo è importante non confondere mai la necessità con la sufficienza di un requisito.
Per sicurezza si può vedere un altro esempio, legato a una situazione di vita reale invece che alla Matematica. “Se rubo del denaro, allora divento un criminale.” La proposizione “se rubo del denaro” è sufficiente perché si diventi un criminale, ma questo può verificarsi anche in casa si compia un omicidio o si sottraggano informazioni anziché denaro.
Condizioni necessarie e sufficienti in Geometria
Nello studio dei teoremi capita spesso di trovare questa espressione. Per esempio considerando i quadrilateri, le CNS perché una figura di quattro lati sia un quadrato è che abbia i lati e le diagonali fra di loro congruenti. Se il poligono che sto considerando soddisfa entrambi questi requisiti infatti può essere solo un quadrato.
Considerando invece i due requisiti descritte in modo separato il discorso cambia. Si tratta infatti di condizioni necessarie, ma da sole non sufficienti per dimostrare che una figura di quattro lati sia un quadrato. Il fatto che un quadrilatero abbia tutti i lati uguali infatti può classificarlo anche come rombo, e avere le diagonali uguali è una proprietà che i quadrati condividono con i rettangoli.
Oppure per quanto riguarda i poligoni regolari. Le condizioni necessarie e sufficienti per cui un poligono sia regolare è che sia equilatero ed equiangolo. Il caso emblematico è quello del triangolo equilatero, che ha tutti e tre i lati congruenti e tutti i suoi angoli sono ampi 60° e quindi uguali fra loro. Lo stesso vale per tutti i poligoni regolari con più di tre alti.
Il fatto che un poligono sia equiangolo come nel caso precedente è solo una condizione necessaria, che da sola non basta a classificarlo come regolare. Idem per quanto riguarda l’avere i lati uguali.