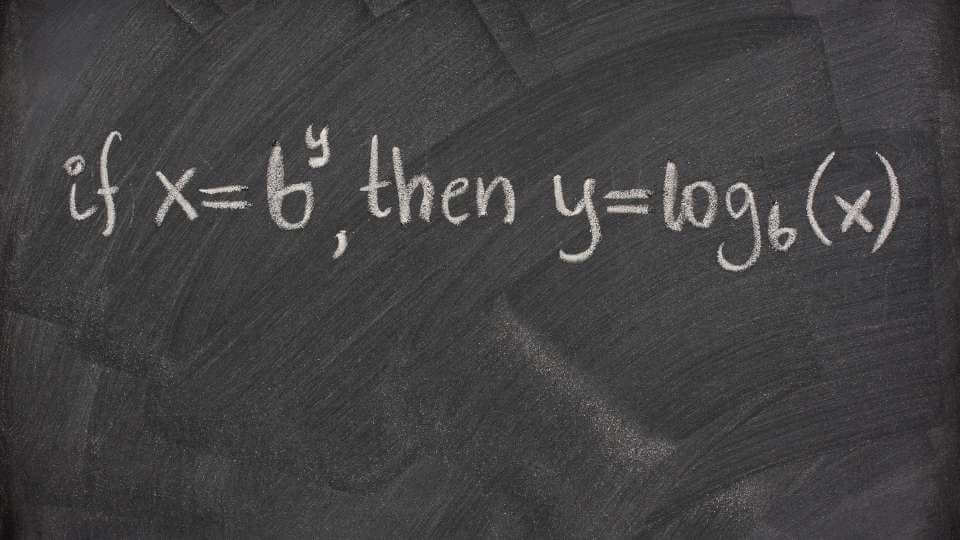Logaritmi: definizione e spiegazione proprietà
In matematica un operatore ricorrente negli integrali e negli studi di funzione è costituito dai logaritmi. Da profani per definirlo in maniera semplice potremmo dire che si tratta dell’inverso del calcolo delle potenze. Non è un operatore utilizzato solo in astratto, ma è fondamentale ad esempio per alcune formule di chimica.
Definizione dei logaritmi
I logaritmi sono operatori matematici indicati come formula grezza con loga(b) = c. In questa formula:
- Innanzitutto la lettera a è detta base del logaritmo ed è sempre un numero reale positivo.
- La lettera b è l’argomento del logaritmo ed è sempre un numero reale positivo.
- La lettera c è il valore del logaritmo.
Il logaritmo naturale
Tra i logaritmi merita un’attenzione particolare quello che è definito logaritmo naturale. Anziché avere come base un numero indicato con il simbolo arabo presenta infatti il valore e. Il logaritmo naturale è definito per ogni valore reale e positivo ma anche per i numeri complessi. Oltre che essere anch’esso utilizzato in formule chimiche e fisiche.
Il simbolo di questo operatore sarebbe comunque log in matematica ( loge in questo caso ) ma solitamente si indica anche con ln.
Tornando al valore di e, si tratta è una costante matematica per convenzione fissata a dodici cifre, 2,718281828459.
Calcolo del logaritmo
Prendiamo ad esempio logcc4
Il risultato è 4. Basta infatti una semplice verifica. Se logcc4 = 4 allora anche ( c )4 = c4 . Come si era visto prima, ac = b.
Le proprietà dei logaritmi: scrittura alternatica, prodotto e rapporto
- Per i logaritmi la prima è la scrittura alternativa. Quando il valore c viene fissato come loga(b), allora si può anche dire che alogab = b. Questa formula può tornare utile durante esercizi particolarmente ostici.
- Passando alle operazioni con i logaritmi, vediamo la regola del logaritmo del prodotto. Se si incontra
loga(b x c) allora il risultato sarà logab + logac. Anziché calcolare solo il logaritmo dell’argomenti finale questo si può distribuire su entrambi i fattori.
- Quando dobbiamo calcolarlo su un rapporto, ad esempio b/c, la regola è simile. Però anziché diluire il logaritmo su una somma lo facciamo su una differenze. La formula è loga(b/c) = logab – logac.
Proprietà dei logaritmi: regola dell’esponente
La formula utilizzata è loga(b)c = cloga. Un caso molto particolare per quanto riguarda gli esponenti è quando se ne incontrano di negativi, In altre parole, i radicali.
In quel caso il coefficiente da sostituire sarà negativo.
Proprietà dei logaritmi: formula del cambiamento di base.
Proprietà dei logaritmi: inversione base – argomento
Un esempio è log713 = 1/log137.